【题目】设关于x的二次方程px2+(p﹣1)x+p+1=0有两个不相等的正根,且一根大于另一根的两倍,求p的取值范围.
参考答案:
【答案】解:关于x的二次方程px2+(p﹣1)x+p+1=0有两个不相等的正根,
则△=(p﹣1)2﹣4p(p+1)=﹣3p2﹣6p+1>0,解得﹣1﹣ ![]() <p<﹣1+
<p<﹣1+ ![]() ,
,
当x1+x2= ![]() >0,及x1x2=
>0,及x1x2= ![]() >0时,方程的两根为正.解之,得0<p<1.故0<p<
>0时,方程的两根为正.解之,得0<p<1.故0<p< ![]() ﹣1.
﹣1.
记x1= 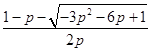 ,x2=
,x2= 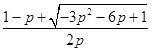 ,
,
由x2>2x1,并注意p>0,得3 ![]() >1﹣p>0,
>1﹣p>0,
∴28p2+52p﹣8<0,即7p2+13p﹣2<0.∴﹣2<p< ![]() .
.
综上得p的取值范围为{p|0<p< ![]() }
}
【解析】根据根与系数的关系和判别式即可求出p的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
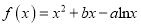 .
.(1)若
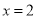 是函数
是函数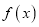 的极值点,1为函数
的极值点,1为函数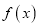 的一个零点,求函数
的一个零点,求函数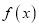 在
在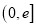 上的最小值.
上的最小值.(2)当
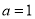 时,函数
时,函数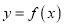 与
与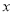 轴在
轴在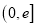 内有两个不同的交点,求
内有两个不同的交点,求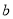 的取值范围.(其中
的取值范围.(其中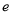 是自然对数的底数)
是自然对数的底数) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c,d∈E,证明下列不等式:
(1)(a2+b2)(c2+d2)≥(ac+bd)2;
(2)a2+b2+c2≥ab+bc+ca. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=ax2+bx+1,a,b∈R,当x=﹣1时,函数f(x)取到最小值,且最小值为0;
(1)求f(x)解析式;
(2)关于x的方程f(x)=|x+1|﹣k+3恰有两个不相等的实数解,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=ax2+bx+c(a≠0),记f[2](x)=f(f(x)),例:f(x)=x2+1,
则f[2](x)=(f(x))2+1=(x2+1)2+1;
(1)f(x)=x2﹣x,解关于x的方程f[2](x)=x;
(2)记△=(b﹣1)2﹣4ac,若f[2](x)=x有四个不相等的实数根,求△的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
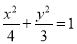 的左顶点为A,右焦点为F,过点F的直线交椭圆于B,C两点.
的左顶点为A,右焦点为F,过点F的直线交椭圆于B,C两点.(1)求该椭圆的离心率;
(2)设直线AB和AC分别与直线x=4交于点M,N,问:x轴上是否存在定点P使得MP⊥NP?若存在,求出点P的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,既是偶函数又在区间(﹣∞,0)上单调递增的是( )
A.f(x)=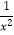
B.f(x)=x2+1
C.f(x)=x
D.f(x)=2x
相关试题

