【题目】已知函数f(x)=m﹣|2x+1|﹣|2x﹣3|,若x0∈R,不等式f(x0)≥0成立,
(1)求实数m的取值范围;
(2)若x+2y﹣m=6,是否存在x,y,使得x2+y2=19成立,若存在,求出x,y值,若不存在,请说明理由.
参考答案:
【答案】
(1)解:由题意可得函数f(x)=m﹣|2x+1|﹣|2x﹣3|≥0有解,即 m≥|2x+1|+|2x﹣3|有解,
故 m大于或等于|2x+1|+|2x﹣3|的最小值.
由于|2x+1|+|2x﹣3|≥|(2x+1)﹣(2x﹣3)|=4,∴m≥4
(2)解:若x+2y﹣m=6,设存在x,y,使得x2+y2=19成立,则圆x2+y2=19和直线x+2y﹣m=6有交点,
即圆心(0,0)到直线x+2y﹣m﹣6=0的距离小于或等于半径 ![]() ,
,
即 ![]() ≤
≤ ![]() ,故当﹣6﹣
,故当﹣6﹣ ![]() ≤m≤﹣6+
≤m≤﹣6+ ![]() 时,圆x2+y2=19和直线x+2y﹣m=6有交点.
时,圆x2+y2=19和直线x+2y﹣m=6有交点.
由 ![]() ,求得
,求得 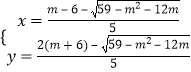 ,或
,或 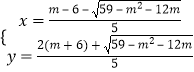
【解析】(1)由题意可得m≥|2x+1|+|2x﹣3|有解,利用绝对值三角不等式求得|2x+1|+|2x﹣3|的最小值,可得m的范围.(2)要使存在x,y,只要圆x2+y2=19和直线x+2y﹣m=6有交点,即圆心(0,0)到直线x+2y﹣m﹣6=0的距离小于或等于半径 ![]() ,由此求得m的范围.再解圆x2+y2=19和直线x+2y﹣m=6组成的方程组,求得直线和圆交点的坐标,即为所求的x、y的值.
,由此求得m的范围.再解圆x2+y2=19和直线x+2y﹣m=6组成的方程组,求得直线和圆交点的坐标,即为所求的x、y的值.
【考点精析】根据题目的已知条件,利用绝对值不等式的解法的相关知识可以得到问题的答案,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知圆O的内接四边形BCED,BC为圆O的直径,BC=2,延长CB,ED交于A点,使得∠DOB=∠ECA,过A作圆O的切线,切点为P,

(1)求证:BD=DE;
(2)若∠ECA=45°,求AP2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,以原点O为极点,x轴正半轴为极轴,建立极坐标系,已知曲线C的参数方程是
 (θ为参数),曲线C与l的交点的极坐标为(2,
(θ为参数),曲线C与l的交点的极坐标为(2,  )和(2,
)和(2,  ),
),
(1)求直线l的普通方程;
(2)设P点为曲线C上的任意一点,求P点到直线l的距离的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(
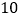 )已知三个点
)已知三个点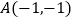 ,
,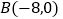 ,
,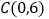 ,圆
,圆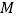 为
为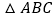 的外接圆.
的外接圆.(
 )求圆
)求圆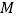 的方程.
的方程.(
 )设直线
)设直线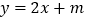 ,与圆
,与圆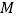 交于
交于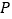 ,
,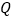 两点,且
两点,且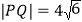 ,求
,求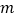 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|0<x<3},B=
 ,则集合A∩(RB)为( )
,则集合A∩(RB)为( )
A.[0,1)
B.(0,1)
C.[1,3)
D.(1,3) -
科目: 来源: 题型:
查看答案和解析>>【题目】(
 分)已知椭圆
分)已知椭圆 的左焦点为
的左焦点为 ,过
,过 的直线
的直线 与
与 交于
交于 、
、 两点.
两点.(
 )求椭圆
)求椭圆 的离心率.
的离心率.(
 )当直线
)当直线 与
与 轴垂直时,求线段
轴垂直时,求线段 的长.
的长.(
 )设线段
)设线段 的中点为
的中点为 ,
, 为坐标原点,直线
为坐标原点,直线 交椭圆
交椭圆 交于
交于 、
、 两点,是否存在直线
两点,是否存在直线 使得
使得 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】执行图题实数的程序框图,如果输入a=2,b=2,那么输出的a值为( )

A.44
B.16
C.256
D.log316
相关试题

