【题目】如图,已知圆O的内接四边形BCED,BC为圆O的直径,BC=2,延长CB,ED交于A点,使得∠DOB=∠ECA,过A作圆O的切线,切点为P,
(1)求证:BD=DE;
(2)若∠ECA=45°,求AP2的值.
参考答案:
【答案】
(1)证明:连结OE,∵圆O的内接四边形BCED,BC为圆O的直径,
BC=2,延长CB,ED交于A点,使得∠DOB=∠ECA,
∴CE∥OD,∴∠CEO=∠EOD,
∵CO=EO,∴∠OCE=∠OEC,
∴∠BOD=∠EOD,
∴BD=DE.
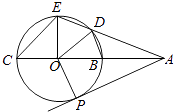
(2)解:解:(2)∵∠ECA=45°,BC为圆O的直径,BC=2,
∴∠COE=90°,∴CE= ![]() ,OD=1,
,OD=1,
∵OD∥CE,∴ ![]() =
= ![]() ,解得AB=
,解得AB= ![]() ,
,
∵过A作圆O的切线,切点为P,
∴AP2=AB(AB+2)= ![]() =2+2
=2+2 ![]()
【解析】(1)连结OE,由已知得CE∥OD,从而∠BOD=∠EOD,由此能证明BD=DE.(2)推导出∠COE=90°,CE= ![]() ,OD=1,AB=
,OD=1,AB= ![]() ,由此利用切割线定理能求出AP2 .
,由此利用切割线定理能求出AP2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知圆
 的圆心在直线
的圆心在直线 上,且过点
上,且过点 ,与直线
,与直线 相切.
相切.(
 )求圆
)求圆 的方程.
的方程.(
 )设直线
)设直线 与圆
与圆 相交于
相交于 ,
, 两点.求实数
两点.求实数 的取值范围.
的取值范围.(
 )在(
)在( )的条件下,是否存在实数
)的条件下,是否存在实数 ,使得弦
,使得弦 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,F是椭圆P:
 (a>b>0)的右焦点,已知A(0,﹣2)与椭圆左顶点关于直线y=x对称,且直线AF的斜率为
(a>b>0)的右焦点,已知A(0,﹣2)与椭圆左顶点关于直线y=x对称,且直线AF的斜率为 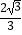 ,
,
(1)求椭圆P的方程;
(2)过点Q(﹣1,0)的直线l交椭圆P于M、N两点,交直线x=﹣4于点E, =
=  ,
,  =
=  ,证明:λ+μ为定值.
,证明:λ+μ为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx,g(x)=
 x2﹣kx;
x2﹣kx;
(1)设k=m+ (m>0),若函数h(x)=f(x)+g(x)在区间(0,2)内有且仅有一个极值点,求实数m的取值范围;
(m>0),若函数h(x)=f(x)+g(x)在区间(0,2)内有且仅有一个极值点,求实数m的取值范围;
(2)设M(x)=f(x)﹣g(x),若函数M(x)存在两个零点x1 , x2(x1>x2),且满足2x0=x1+x2 , 问:函数M(x)在(x0 , M(x0))处的切线能否平行于直线y=1,若能,求出该切线方程,若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,以原点O为极点,x轴正半轴为极轴,建立极坐标系,已知曲线C的参数方程是
 (θ为参数),曲线C与l的交点的极坐标为(2,
(θ为参数),曲线C与l的交点的极坐标为(2,  )和(2,
)和(2,  ),
),
(1)求直线l的普通方程;
(2)设P点为曲线C上的任意一点,求P点到直线l的距离的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(
 )已知三个点
)已知三个点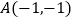 ,
,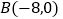 ,
,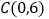 ,圆
,圆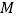 为
为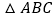 的外接圆.
的外接圆.(
 )求圆
)求圆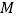 的方程.
的方程.(
 )设直线
)设直线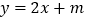 ,与圆
,与圆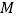 交于
交于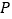 ,
,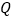 两点,且
两点,且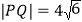 ,求
,求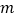 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=m﹣|2x+1|﹣|2x﹣3|,若x0∈R,不等式f(x0)≥0成立,
(1)求实数m的取值范围;
(2)若x+2y﹣m=6,是否存在x,y,使得x2+y2=19成立,若存在,求出x,y值,若不存在,请说明理由.
相关试题

