【题目】已知函数f(x)=x3﹣2x2﹣4x.
(1)求函数y=f(x)的单调区间;
(2)求函数f(x)在区间[﹣1,4]上的最大值和最小值.
参考答案:
【答案】
(1)解:∵函数f(x)=x3﹣2x2﹣4x,
∴f′(x)=3x2﹣4x﹣4,
由f′(x)>0,得x<﹣ ![]() 或x>2,
或x>2,
由f′(x)<0,得﹣ ![]() <x<2,
<x<2,
∴函数y=f(x)的单调增区间是(﹣∞,﹣ ![]() ),[2,+∞);单调减区间是[﹣
),[2,+∞);单调减区间是[﹣ ![]() ,2].
,2].
(2)解:由f′(x)=3x2﹣4x﹣4=0,
得 ![]() ,x2=2,
,x2=2,
列表,得:
x | ﹣1 | (﹣1,﹣ | ﹣ | (﹣ | 2 | (2,4) | 4 |
f′(x) | + | 0 | ﹣ | 0 | + | ||
f(x) | 1 | ↑ |
| ↓ | ﹣8 | ↑ | 16 |
∴f(x)在[﹣1,4]上的最大值为f(x)max=f(4)=16,最小值为f(x)min=f(2)=﹣8.
【解析】(1)求出f′(x)=3x2﹣4x﹣4,利用导数性质能求出函数y=f(x)的单调增区间和单调减区间.(2)由f′(x)=3x2﹣4x﹣4=0,得 ![]() ,x2=2,列表讨论能求出f(x)在[﹣1,4]上的最大值和最小值.
,x2=2,列表讨论能求出f(x)在[﹣1,4]上的最大值和最小值.
【考点精析】掌握利用导数研究函数的单调性和函数的最大(小)值与导数是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业投资1千万元用于一个高科技项目,每年可获利25%.由于企业间竞争激烈,每年底需要从利润中取出资金200万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.经过多少年后,该项目的资金可以达到4倍的目标?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)=x3+(k﹣1)x2+(k+5)x﹣1在区间(0,2)上不单调,则实数k的取值范围为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形
 中,
中, ,
, 是边长为l的正方形,平面
是边长为l的正方形,平面 底面
底面 ,若
,若 分别是
分别是 的中点.
的中点.(1)求证:
 底面
底面 ;
;(2)求几何体
 的体积.
的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的首项a1=1,前n项和Sn满足关系式:3tSn﹣(2t+3)Sn﹣1=3t(t>0,n=2,3,4…)
(1)求证:数列{an}是等比数列;
(2)设数列{an}的公比为f(t),作数列{bn},使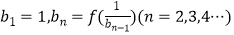 ,求数列{bn}的通项bn;
,求数列{bn}的通项bn;
(3)求和:b1b2﹣b2b3+b3b4﹣b4b5+…+b2n﹣1b2n﹣b2nb2n+1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{bn}满足bn=|
 |,其中a1=2,an+1=
|,其中a1=2,an+1=  .
.
(1)求b1 , b2 , b3 , 并猜想bn的表达式(不必写出证明过程);
(2)由(1)写出数列{bn}的前n项和Sn , 并用数学归纳法证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】广场舞是现代城市群众文化、娱乐发展的产物,也是城市精神文明建设成果的一个重要象征.2016年某校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:
 ,
, ,
, ,
, ,
, ,
, 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.(l)计算这40名广场舞者中年龄分布在
 的人数;
的人数;(2)若从年龄在
 中的广场舞者任取2名,求这两名广场舞者中恰有一人年龄在
中的广场舞者任取2名,求这两名广场舞者中恰有一人年龄在 的概率.
的概率.
相关试题

