【题目】某企业投资1千万元用于一个高科技项目,每年可获利25%.由于企业间竞争激烈,每年底需要从利润中取出资金200万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.经过多少年后,该项目的资金可以达到4倍的目标?
参考答案:
【答案】解:设第n年终资金为an万元,由题意可得an=(1+25%)an﹣1﹣200(n≥2),变形整理可得:an﹣800= ![]() (an﹣1﹣800),
(an﹣1﹣800),
故{an﹣800}构成一个等比数列,a1=1000(1+25%)﹣200=1050,a1﹣800=250,
∴an﹣800=250× ![]() ,
,
令an≥4000,得 ![]() ≥16,两边取对数可得:n≥
≥16,两边取对数可得:n≥ ![]() ≈13,
≈13,
故至少要13年才能达到目标
【解析】设第n年终资金为an万元,由题意可得an=(1+25%)an﹣1﹣200(n≥2),变形整理可得:an﹣800= ![]() (an﹣1﹣800),利用等比数列的通项公式可得an , 进而得出.
(an﹣1﹣800),利用等比数列的通项公式可得an , 进而得出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某基建公司年初以100万元购进一辆挖掘机,以每年22万元的价格出租给工程队.基建公司负责挖掘机的维护,第一年维护费为2万元,随着机器磨损,以后每年的维护费比上一年多2万元,同时该机器第x(x∈N* , x≤16)年末可以以(80﹣5x)万元的价格出售.
(1)写出基建公司到第x年末所得总利润y(万元)关于x(年)的函数解析式,并求其最大值;
(2)为使经济效益最大化,即年平均利润最大,基建公司应在第几年末出售挖掘机?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=(ex﹣1)(x﹣1)k , k∈N* , 若函数y=f(x)在x=1处取到极小值,则k的最小值为( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是边长2的正方形,E,F分别为线段DD1 , BD的中点.
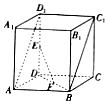
(1)求证:EF∥平面ABC1D1;
(2)AA1=2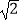 ,求异面直线EF与BC所成的角的大小.
,求异面直线EF与BC所成的角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)=x3+(k﹣1)x2+(k+5)x﹣1在区间(0,2)上不单调,则实数k的取值范围为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形
 中,
中, ,
, 是边长为l的正方形,平面
是边长为l的正方形,平面 底面
底面 ,若
,若 分别是
分别是 的中点.
的中点.(1)求证:
 底面
底面 ;
;(2)求几何体
 的体积.
的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3﹣2x2﹣4x.
(1)求函数y=f(x)的单调区间;
(2)求函数f(x)在区间[﹣1,4]上的最大值和最小值.
相关试题

