【题目】广场舞是现代城市群众文化、娱乐发展的产物,也是城市精神文明建设成果的一个重要象征.2016年某校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.
(l)计算这40名广场舞者中年龄分布在![]() 的人数;
的人数;
(2)若从年龄在![]() 中的广场舞者任取2名,求这两名广场舞者中恰有一人年龄在
中的广场舞者任取2名,求这两名广场舞者中恰有一人年龄在![]() 的概率.
的概率.

参考答案:
【答案】(1)30;(2)![]() .
.
【解析】试题分析:(1)由题意可知,样本容量为40,由条形图可求得![]() 的频率和为
的频率和为![]() ,所以n=频率
,所以n=频率![]() 样本容量。(2)由直方图可知,年龄在
样本容量。(2)由直方图可知,年龄在![]() 有2人,分别记为
有2人,分别记为![]() ,在
,在![]() 有4人,分别记为
有4人,分别记为![]() .采用枚举法,可知总共情况是15种,满足条件的是8种,所以概率为
.采用枚举法,可知总共情况是15种,满足条件的是8种,所以概率为![]() 。
。
试题解析:(1)由表中数据知,这40名广场舞者中年龄分布在![]() 的人数为
的人数为![]() .
.
(2)由直方图可知,年龄在![]() 有2人,分别记为
有2人,分别记为![]() ,在
,在![]() 有4人,分别记为
有4人,分别记为![]() .
.
现从这6人中任选两人,共有如下15种选法:,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
其中恰有1人在![]() 有8种,
有8种,
故这两名广场舞者恰有一人年龄在![]() 的概率为
的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3﹣2x2﹣4x.
(1)求函数y=f(x)的单调区间;
(2)求函数f(x)在区间[﹣1,4]上的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的首项a1=1,前n项和Sn满足关系式:3tSn﹣(2t+3)Sn﹣1=3t(t>0,n=2,3,4…)
(1)求证:数列{an}是等比数列;
(2)设数列{an}的公比为f(t),作数列{bn},使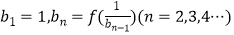 ,求数列{bn}的通项bn;
,求数列{bn}的通项bn;
(3)求和:b1b2﹣b2b3+b3b4﹣b4b5+…+b2n﹣1b2n﹣b2nb2n+1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{bn}满足bn=|
 |,其中a1=2,an+1=
|,其中a1=2,an+1=  .
.
(1)求b1 , b2 , b3 , 并猜想bn的表达式(不必写出证明过程);
(2)由(1)写出数列{bn}的前n项和Sn , 并用数学归纳法证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
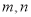 是空间两条直线,
是空间两条直线, 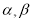 是空间两个平面,则下列命题中不正确的是( )
是空间两个平面,则下列命题中不正确的是( )A. 当
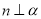 时,“
时,“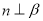 ”是“
”是“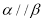 ”的充要条件
”的充要条件B. 当
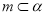 时,“
时,“ ”是“
”是“ ”的充分不必要条件
”的充分不必要条件C. 当
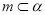 时,“
时,“ ”是“
”是“ ”的必要不充分条件
”的必要不充分条件D. 当
 时,“
时,“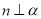 ”是“
”是“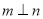 ”的充分不必要条件
”的充分不必要条件 -
科目: 来源: 题型:
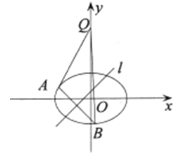
查看答案和解析>>【题目】已知椭圆
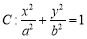
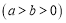 的焦距为2,离心率为
的焦距为2,离心率为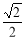 ,
,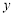 轴上一点
轴上一点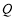 的坐标为
的坐标为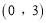 .
.
(Ⅰ)求该椭圆的方程;
(Ⅱ)若对于直线
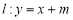 ,椭圆
,椭圆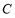 上总存在不同的两点
上总存在不同的两点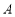 与
与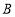 关于直线
关于直线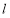 对称,且
对称,且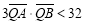 ,求
,求实数
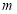 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,射线y=x(x≥0)和y=0(x≥0)上分别依次有点A1、A2 , …,An , …,和点B1 , B2 , …,Bn…,其中
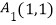 ,
, 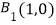 ,
, 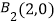 .且
.且 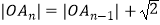 ,
, 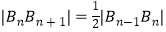 (n=2,3,4…).
(n=2,3,4…). 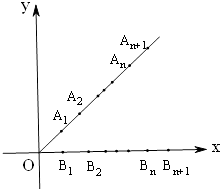
(1)用n表示|OAn|及点An的坐标;
(2)用n表示|BnBn+1|及点Bn的坐标;
(3)写出四边形AnAn+1Bn+1Bn的面积关于n的表达式S(n),并求S(n)的最大值.
相关试题

