【题目】如图,三角形![]() 中,
中,![]() ,
,![]() 是边长为l的正方形,平面
是边长为l的正方形,平面![]() 底面
底面![]() ,若
,若![]() 分别是
分别是![]() 的中点.
的中点.
(1)求证:![]() 底面
底面![]() ;
;
(2)求几何体![]() 的体积.
的体积.

参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)通过面面平行证明线面平行,所以取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() .只需通过证明HG//BC,HF//AB来证明面GHF//面ABC,从而证明
.只需通过证明HG//BC,HF//AB来证明面GHF//面ABC,从而证明![]() 底面
底面![]() 。
。
(2)原图形可以看作是以点C为顶点,ABDE为底的四棱锥,所四棱锥的体积公式可求得体积。
试题解析:(1)取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() .(如图)
.(如图)
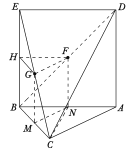
∵![]() 分别是
分别是![]() 和
和![]() 的中点,
的中点,
∴![]() ,且
,且![]() ,
,
![]() ,且
,且![]() .
.
又∵![]() 为正方形,∴
为正方形,∴![]() ,
,![]() .
.
∴![]() 且
且![]() .
.
∴![]() 为平行四边形.
为平行四边形.
∴![]() ,又
,又![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)因为![]() ,∴
,∴![]() ,
,
又平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
∵三角形![]() 是等腰直角三角形,∴
是等腰直角三角形,∴![]() .
.
∵![]() 是四棱锥,
是四棱锥,
∴![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是边长2的正方形,E,F分别为线段DD1 , BD的中点.
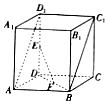
(1)求证:EF∥平面ABC1D1;
(2)AA1=2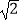 ,求异面直线EF与BC所成的角的大小.
,求异面直线EF与BC所成的角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业投资1千万元用于一个高科技项目,每年可获利25%.由于企业间竞争激烈,每年底需要从利润中取出资金200万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.经过多少年后,该项目的资金可以达到4倍的目标?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)=x3+(k﹣1)x2+(k+5)x﹣1在区间(0,2)上不单调,则实数k的取值范围为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3﹣2x2﹣4x.
(1)求函数y=f(x)的单调区间;
(2)求函数f(x)在区间[﹣1,4]上的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的首项a1=1,前n项和Sn满足关系式:3tSn﹣(2t+3)Sn﹣1=3t(t>0,n=2,3,4…)
(1)求证:数列{an}是等比数列;
(2)设数列{an}的公比为f(t),作数列{bn},使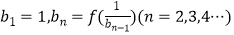 ,求数列{bn}的通项bn;
,求数列{bn}的通项bn;
(3)求和:b1b2﹣b2b3+b3b4﹣b4b5+…+b2n﹣1b2n﹣b2nb2n+1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{bn}满足bn=|
 |,其中a1=2,an+1=
|,其中a1=2,an+1=  .
.
(1)求b1 , b2 , b3 , 并猜想bn的表达式(不必写出证明过程);
(2)由(1)写出数列{bn}的前n项和Sn , 并用数学归纳法证明.
相关试题

