【题目】已知函数![]() .
.
(1)求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,求证:
时,求证:![]() ;
;
(3)若![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】试题分析: (1)先由导数几何意义得切线斜率,再根据点斜式求切线方程,(2)构造差函数:![]() ,再利用导数求其最小值
,再利用导数求其最小值![]() ,即得证,(3)先变量分离,将不等式恒成立问题转化为求对应函数最值问题:
,即得证,(3)先变量分离,将不等式恒成立问题转化为求对应函数最值问题:![]() ,其中
,其中![]() ,再利用导数求其最小值
,再利用导数求其最小值![]() ,可得实数
,可得实数![]() 的取值范围.
的取值范围.
试题解析:(1)![]() ,
,![]() ,
,
∴![]() ,
,
又切点坐标为![]() ,故所求切线方程为
,故所求切线方程为![]()
(2)令![]() ,
,
令![]() ,得
,得![]() ,
,
∴当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增
单调递增
∴![]() ,从而
,从而![]() .
.
(3)![]() 对任意的
对任意的![]() 恒成立
恒成立![]() 对任意的
对任意的![]() 恒成立
恒成立
令![]() ,
,
∴![]()
由(2)可知当![]() 时,
时,![]() 恒成立,
恒成立,
令![]() ,得
,得![]() ;
;![]() ,得
,得![]()
∴![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ,
,![]()
∴![]()
∴实数![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解
 两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).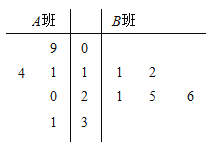
(1)分别求出图中所给两组样本数据的平均值,并据此估计哪个班的学生平均观看的时间较长;
(2)从
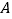 班的样本数据中随机抽取一个不超过19的数据记为
班的样本数据中随机抽取一个不超过19的数据记为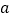 ,从
,从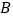 班的样本数据中随机抽取一个不超过21的数据记为
班的样本数据中随机抽取一个不超过21的数据记为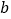 ,求
,求 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某少数民族的刺绣有着悠久的历史,下图
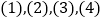 为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含
为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含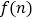 个小正方形.
个小正方形.
(1)求出
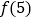 ;
;(2)利用合情推理的“归纳推理思想”归纳出
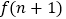 与
与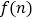 的关系式,
的关系式,(3)根据你得到的关系式求
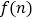 的表达式
的表达式 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
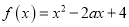 ,在下列条件下,求实数
,在下列条件下,求实数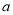 的取值范围.
的取值范围.(1)零点均大于
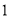 ;
;(2)一个零点大于
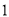 ,一个零点小于
,一个零点小于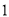 ;
;(3)一个零点在
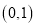 内,另一个零点在
内,另一个零点在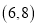 内.
内. -
科目: 来源: 题型:
查看答案和解析>>【题目】在下图所示的几何体中,底面
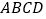 为正方形,
为正方形,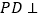 平面
平面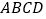 ,
,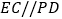 ,且
,且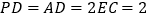 ,
,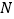 为线段
为线段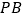 的中点.
的中点.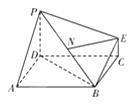
(1)证明:
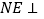 平面
平面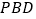 ;
;(2)求四棱锥
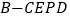 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
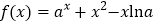
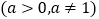 .
.(1)当
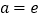 时,判断函数
时,判断函数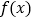 的单调性;
的单调性;(2)若存在
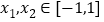 ,使得
,使得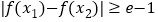 (
(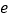 是自然对数的底数),求实数
是自然对数的底数),求实数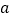 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年夏季奥运会将在巴西里约热内卢举行,体育频道为了解某地区关于
奥运会直播的收视情况,随机抽取了
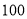 名观众进行调查,其中
名观众进行调查,其中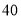 岁以上的观众有
岁以上的观众有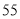 名,下面是根据
名,下面是根据调查结果绘制的观众准备平均每天收看奥运会直播时间的频率分布表(时间:分钟):
分组
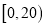


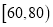
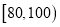
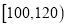
频率
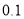
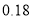
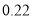
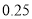
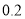
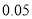
将每天准备收看奥运会直播的时间不低于
 分钟的观众称为“奥运迷”,已知“奥运迷”中有
分钟的观众称为“奥运迷”,已知“奥运迷”中有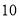 名
名 岁
岁以上的观众.
(1)根据已知条件完成下面的
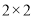 列联表,并据此资料你是否有
列联表,并据此资料你是否有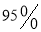 以上的把握认为“奥运迷”与年龄
以上的把握认为“奥运迷”与年龄有关?
非“奥运迷”
“奥运迷”
合计
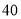 岁以下
岁以下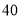 岁以上
岁以上合计
(2)将每天准备收看奥运会直播不低于
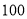 分钟的观众称为“超级奥运迷”,已知“超级奥运迷”中有
分钟的观众称为“超级奥运迷”,已知“超级奥运迷”中有
名
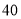 岁以上的观众,若从“超级奥运迷”中任意选取
岁以上的观众,若从“超级奥运迷”中任意选取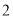 人,求至少有
人,求至少有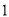 名
名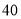 岁以上的观众的概率.
岁以上的观众的概率.附:

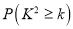
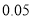
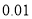
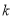
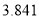

相关试题

