【题目】某校为了了解![]() 两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
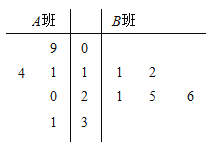
(1)分别求出图中所给两组样本数据的平均值,并据此估计哪个班的学生平均观看的时间较长;
(2)从![]() 班的样本数据中随机抽取一个不超过19的数据记为
班的样本数据中随机抽取一个不超过19的数据记为![]() ,从
,从![]() 班的样本数据中随机抽取一个不超过21的数据记为
班的样本数据中随机抽取一个不超过21的数据记为![]() ,求
,求![]() 的概率.
的概率.
参考答案:
【答案】(1)![]() 班学生平均观看时间较长;(2)
班学生平均观看时间较长;(2)![]() .
.
【解析】试题分析: (1)先根据平均数等于总数除以样本个数,计算两班平均值,再比较大小即可,(2)利用枚举法计算样本总数为9种,再从中计算满足![]() 的样本数,最后根据古典概型概率公式求概率.
的样本数,最后根据古典概型概率公式求概率.
试题解析:(1)![]() 班样本数据的平均值为
班样本数据的平均值为![]()
由此估计![]() 班学生平均观看时间大约为17小时,
班学生平均观看时间大约为17小时,
![]() 班样本数据的平均值为
班样本数据的平均值为![]() ,
,
由此估计![]() 班学生平均观看时间较长.
班学生平均观看时间较长.
(2)![]() 班的样本数据中不超过19的数据
班的样本数据中不超过19的数据![]() 有3个,分别为:9,11,14,
有3个,分别为:9,11,14,
![]() 班的样本数据中不超过21的数据
班的样本数据中不超过21的数据![]() 有3个,分别为:11,12,21,
有3个,分别为:11,12,21,
从![]() 班和
班和![]() 班的样本数据中各随机抽取一个共有9种不同情况,分别为:
班的样本数据中各随机抽取一个共有9种不同情况,分别为:![]()
其中![]() 的情况有
的情况有![]() 两种,
两种,
故![]() 的概率为
的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究。他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子的发芽数,得到如下资料:
日期
12月1日
12月2日
12月3日
12月4日
12月5日
温差
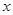 /
/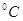
10
11
13
12
8
发芽数
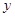 /颗
/颗23
25
30
26
16
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程
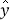 =bx+a;
=bx+a;(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为 得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
(附:
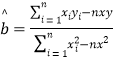 ,
,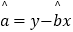 ,其中
,其中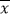 ,
,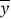 为样本平均值)
为样本平均值) -
科目: 来源: 题型:
查看答案和解析>>【题目】随机掷两枚质地均匀的骰子,它们向上的点数之和不超过5的概率记为p1,点数之和大于5的概率记为p2,点数之和为偶数的概率记为p3,则
( )
A. p1<p2<p3 B. p2<p1<p3 C. p1<p3<p2 D. p3<p1<p2
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数
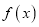 ,若存在
,若存在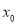 ,使
,使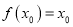 成立,则称
成立,则称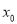 为函数
为函数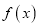 的不动点,已知
的不动点,已知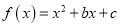 .
.(1)若
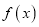 有两个不动点为
有两个不动点为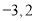 ,求函数
,求函数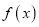 的零点;
的零点;(2)若
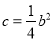 时,函数
时,函数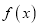 没有不动点,求实数
没有不动点,求实数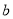 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某少数民族的刺绣有着悠久的历史,下图
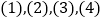 为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含
为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含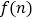 个小正方形.
个小正方形.
(1)求出
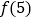 ;
;(2)利用合情推理的“归纳推理思想”归纳出
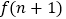 与
与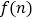 的关系式,
的关系式,(3)根据你得到的关系式求
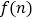 的表达式
的表达式 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
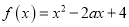 ,在下列条件下,求实数
,在下列条件下,求实数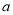 的取值范围.
的取值范围.(1)零点均大于
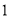 ;
;(2)一个零点大于
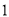 ,一个零点小于
,一个零点小于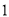 ;
;(3)一个零点在
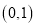 内,另一个零点在
内,另一个零点在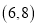 内.
内. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
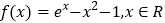 .
.(1)求函数
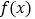 的图象在点
的图象在点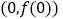 处的切线方程;
处的切线方程;(2)当
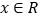 时,求证:
时,求证: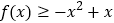 ;
;(3)若
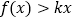 对任意的
对任意的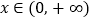 恒成立,求实数
恒成立,求实数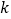 的取值范围.
的取值范围.
相关试题

