【题目】已知函数 ![]() .
.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)对任意 ![]() ,都有xln(kx)﹣kx+1≤mx,求m的取值范围.
,都有xln(kx)﹣kx+1≤mx,求m的取值范围.
参考答案:
【答案】解:由已知得,f(x)的定义域为(0,+∞).
(Ⅰ) ![]() ,.
,.
令f'(x)>0,得x>1,令f'(x)<0,得0<x<1.
所以函数f(x)的单调减区间是(0,1),单调增区间是(1,+∞),
(Ⅱ)由xln(kx)﹣kx+1≤mx,
得 ![]() ,即m≥f(x)max .
,即m≥f(x)max .
由(Ⅰ)知,
(i)当k≥2时,f(x)在 ![]() 上单调递减,所以
上单调递减,所以 ![]() ,所以m≥0;.
,所以m≥0;.
(ii)当0<k≤1时,f(x)在 ![]() 上单调递增,所以
上单调递增,所以 ![]() ,
,
所以 ![]() ;
;
(iii)当1<k<2时,f(x)在 ![]() 上单调递减,在
上单调递减,在 ![]() 上单调递增,
上单调递增,
所以 ![]() .
.
又 ![]() ,
, ![]() ,
,
①若 ![]() ,即
,即 ![]() ,所以1<k<2ln2,此时
,所以1<k<2ln2,此时 ![]() ,
,
所以 ![]() .
.
②若 ![]() ,即
,即 ![]() ,所以2ln2≤k<2,此时f(x)max=0,所以m≥0
,所以2ln2≤k<2,此时f(x)max=0,所以m≥0
综上所述,当k≥2ln2时,m≥0;
当0<k<2ln2时, ![]() .
.
【解析】(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间;(Ⅱ)问题转化为m≥f(x)max , 通过讨论k的范围,求出f(x)的最大值,从而求出m的范围即可.
【考点精析】关于本题考查的利用导数研究函数的单调性和函数的最大(小)值与导数,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.
比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
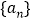 为等差数列,
为等差数列, ,
,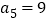 .
.(1) 求数列
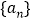 的通项公式;
的通项公式;(2)求数列
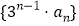 的前n项和
的前n项和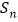 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平面五边形ABCDE中,AB∥CD,∠BAD=90°,AB=2,CD=1,△ADE是边长为2的正三角形.现将△ADE沿AD折起,得到四棱锥E﹣ABCD(如图2),且DE⊥AB.
(Ⅰ)求证:平面ADE⊥平面ABCD;
(Ⅱ)求平面BCE和平面ADE所成锐二面角的大小;
(Ⅲ)在棱AE上是否存在点F,使得DF∥平面BCE?若存在,求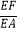 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.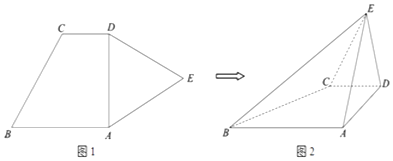
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司购买了A,B,C三种不同品牌的电动智能送风口罩.为了解三种品牌口罩的电池性能,现采用分层抽样的方法,从三种品牌的口罩中抽出25台,测试它们一次完全充电后的连续待机时长,统计结果如下(单位:小时):
A
4
4
4.5
5
5.5
6
6
B
4.5
5
6
6.5
6.5
7
7
7.5
C
5
5
5.5
6
6
7
7
7.5
8
8
(1)已知该公司购买的C品牌电动智能送风口罩比B品牌多200台,求该公司购买的B品牌电动智能送风口罩的数量;
(2)从A品牌和B品牌抽出的电动智能送风口罩中,各随机选取一台,求A品牌待机时长高于B品牌的概率;
(3)再从A,B,C三种不同品牌的电动智能送风口罩中各随机抽取一台,它们的待机时长分别是a,b,c(单位:小时).这3个新数据与表格中的数据构成的新样本的平均数记为μ1 , 表格中数据的平均数记为μ0 . 若μ0≤μ1 , 写出a+b+c的最小值(结论不要求证明). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知从椭圆
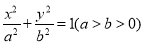 的一个焦点看两短轴端点所成视角为
的一个焦点看两短轴端点所成视角为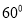 ,且椭圆经过
,且椭圆经过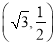 .
.(1)求椭圆的方程;
(2)是否存在实数
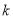 ,使直线
,使直线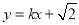 与椭圆有两个不同交点
与椭圆有两个不同交点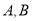 ,且
,且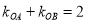 (
(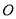 为坐标原点),若存在,求出
为坐标原点),若存在,求出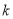 的值.不存在,说明理由.
的值.不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知
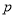 :“直线
:“直线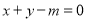 与圆
与圆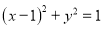 相交”;
相交”; 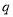 :“
:“ 有一正根和一负根”.若
有一正根和一负根”.若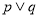 为真,
为真, 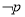 为真,求
为真,求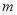 的取值范围.
的取值范围.(2)已知椭圆
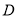 :
: 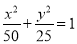 与圆
与圆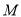 :
:  ,双曲线
,双曲线 与椭圆
与椭圆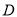 有相同的焦点,它的两条渐近线恰好与圆
有相同的焦点,它的两条渐近线恰好与圆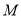 相切.求双曲线
相切.求双曲线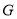 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 与
与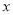 轴负半轴相交于点
轴负半轴相交于点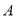 ,与
,与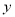 轴正半轴相交于点
轴正半轴相交于点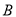 .
.(1)若过点
 的直线
的直线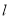 被圆
被圆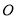 截得的弦长为
截得的弦长为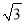 ,求直线
,求直线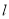 的方程;
的方程;(2)若在以
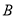 为圆心半径为
为圆心半径为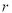 的圆上存在点
的圆上存在点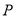 ,使得
,使得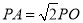 (
(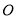 为坐标原点),求
为坐标原点),求 的取值范围;
的取值范围;(3)设
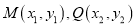 是圆
是圆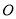 上的两个动点,点
上的两个动点,点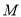 关于原点的对称点为
关于原点的对称点为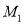 ,点
,点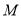 关于
关于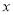 轴的对称点为
轴的对称点为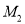 ,如果直线
,如果直线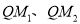 与
与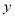 轴分别交于
轴分别交于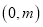 和
和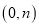 ,问
,问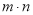 是否为定值?若是求出该定值;若不是,请说明理由.
是否为定值?若是求出该定值;若不是,请说明理由.
相关试题

