【题目】在平面直角坐标系中,直线L的参数方程为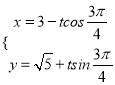 (
(![]() 为参数).在以原点
为参数).在以原点 ![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标中,圆C的方程为
轴正半轴为极轴的极坐标中,圆C的方程为![]() .
.
(Ⅰ)写出直线L的倾斜角![]() 和圆C的直角坐标方程;
和圆C的直角坐标方程;
(Ⅱ)若点 P坐标为![]() ,圆C与直线L交于 A,B两点,求|PA|
,圆C与直线L交于 A,B两点,求|PA|![]() |PB|的值.
|PB|的值.
的值.
参考答案:
【答案】(1)![]() (2)4
(2)4
【解析】试题分析:(Ⅰ)直线![]() 的普通方程为
的普通方程为![]() ;左右两边同乘
;左右两边同乘![]() ,再利用公式求得圆
,再利用公式求得圆![]() 方程为
方程为![]() ;(Ⅱ)把直线
;(Ⅱ)把直线![]() 的参数方程代入圆
的参数方程代入圆![]() 的直角坐标方程,再利用韦达定理和参数的几何意义可得
的直角坐标方程,再利用韦达定理和参数的几何意义可得![]() .
.
试题解析:
解:(Ⅰ)直线L的普通方程为x+y﹣3+![]() =0,∴
=0,∴![]() ;
;
又由![]() 得 ρ2=2
得 ρ2=2![]() ρsinθ,化为直角坐标方程为x2+(y﹣
ρsinθ,化为直角坐标方程为x2+(y﹣![]() )2=5;
)2=5;
(Ⅱ)把直线L的参数方程代入圆C的直角坐标方程,
得t2+3![]() t+4=0
t+4=0
设t1,t2是上述方程的两实数根,
又直线L过点P![]() ,A、B两点对应的参数分别为t1,t2,
,A、B两点对应的参数分别为t1,t2,
所以|PA|![]() |PB|=4.
|PB|=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面给出四种说法:
①用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;
②命题P:“x0∈R,x02﹣x0﹣1>0”的否定是¬P:“x∈R,x2﹣x﹣1≤0”;
③设随机变量X服从正态分布N(0,1),若P(x>1)=p则P(﹣1<X<0)=
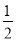 ﹣p
﹣p④回归直线一定过样本点的中心(
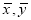 ).
).其中正确的说法有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数
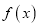 ,若存在实数对(
,若存在实数对(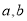 ),使得等式
),使得等式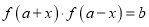 对定义域中的每一个
对定义域中的每一个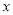 都成立,则称函数
都成立,则称函数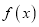 是“(
是“(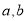 )型函数”.
)型函数”.(1) 判断函数
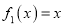 是否为 “(
是否为 “(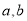 )型函数”,并说明理由;
)型函数”,并说明理由;(2) 若函数
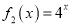 是“(
是“(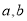 )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对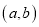 ;
;(3)已知函数
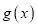 是“(
是“(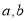 )型函数”,对应的实数对
)型函数”,对应的实数对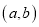 为(1,4).当
为(1,4).当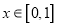 时,
时, 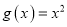
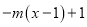
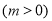 ,若当
,若当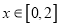 时,都有
时,都有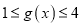 ,试求
,试求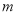 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋中有7个大小、形状相同的小球,6个白球1个红球.现任取1个,若为红球就停止,若为白球就放回,搅拌均匀后再接着取.试设计一个模拟试验,计算恰好第三次摸到红球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着移动互联网时代的到来,手机的使用非常普遍,“低头族”随处可见。某校为了解家长和教师对学生带手机进校园的态度,随机调查了100位家长和教师,得到情况如下表:
教师
家长
反对
40
20
支持
20
20
(1)是否有95%以上的把握认为“带手机进校园与身份有关”,并说明理由;
(2)把以上频率当概率,随机抽取3位教师,记其中反对学生带手机进校园的人数为X,求随机变量X的分布列和数学期望.
附:
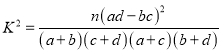
P(K2≥k0)
0.050
0.010
0.001
k0
3.841
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两种商品,经营销售这两种商品所得的利润依次为M万元和N万元,它们与投入资金
 万元的关系可由经验公式给出:M=
万元的关系可由经验公式给出:M= ,N=
,N= (
( ≥1).今有8万元资金投入经营甲、乙两种商品,且乙商品至少要求投资1万元,
≥1).今有8万元资金投入经营甲、乙两种商品,且乙商品至少要求投资1万元,设投入乙种商品的资金为
 万元,总利润
万元,总利润 ;
;(2)为获得最大利润,对甲、乙两种商品的资金投入分别是多少?共能获得多大利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出下列函数的单调区间.
(1)y=|x+1|; (2)y=-x2+ax;
(3)y=|2x-1|; (4)y=-
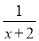 .
.
相关试题

