【题目】如图,四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() .
.
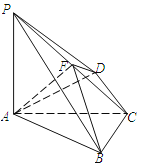
(1)求![]() 的长;
的长;
(2)求二面角![]() 的正弦值.
的正弦值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)连接![]() 交
交![]() 于点
于点![]() ,等腰三角形
,等腰三角形![]() 中利用“三线合一”证出
中利用“三线合一”证出![]() ,因此分别以
,因此分别以![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴建立空间直角坐标系如图所示.结合题意算出
轴建立空间直角坐标系如图所示.结合题意算出![]() 、
、![]() 、
、![]() 、
、![]()
各点的坐标,设![]() ,根据
,根据![]() 为
为![]() 边的中点且
边的中点且![]() ,算出
,算出![]() ,从而得到
,从而得到![]() ,可得
,可得![]() 的长;(2)由(1)的计算,得
的长;(2)由(1)的计算,得![]() ,
,![]() ,
,![]() .利用垂直向量数量积为零的方法建立方程组,解出
.利用垂直向量数量积为零的方法建立方程组,解出![]() 和
和![]() 分别为平面
分别为平面![]() 、平面
、平面![]() 的法向量,利用空间向量的夹角公式算出
的法向量,利用空间向量的夹角公式算出![]() 、
、![]() 夹角的余弦,结合同角三角函数的平方关系即可算出二面角
夹角的余弦,结合同角三角函数的平方关系即可算出二面角![]() 的正弦值.
的正弦值.
试题解析:(1)如图,连接![]() 交
交![]() 于点
于点![]() ,
,
∵![]() ,
,![]() 平分角
平分角![]() ,∴
,∴![]() ,
,
以![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,
,
则![]() ,而
,而![]() ,可得
,可得![]() ,
,
又∵![]() ,
,
∴可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由于![]() ⊥底面
⊥底面![]() ,可设
,可设![]() ,
,
∵![]() 为
为![]() 边的中点,∴
边的中点,∴![]() ,由此可得
,由此可得![]() ,
,
∵![]() ,且
,且![]() ,
,
∴![]() ,解得
,解得![]() (舍负),
(舍负),
因此,![]() ,可得
,可得![]() 的长为
的长为![]() .
.
(2)由(1)知![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,
,
∵![]() ,且
,且![]() ,∴,取
,∴,取![]() ,得
,得![]() ,
,
同理,由![]() 且
且![]() ,解出
,解出![]() .
.
∴向量![]() ,
,![]() 的夹角余弦值为
的夹角余弦值为![]()
![]() ,
,
因此,二面角![]() 的正弦值等于
的正弦值等于![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
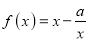 (
(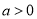 ),
),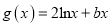 ,且直线
,且直线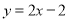 与曲线
与曲线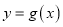 相切.
相切.(1)求
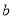 的值;
的值;(2)若对
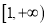 内的一切实数
内的一切实数 ,不等式
,不等式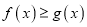 恒成立,求实数
恒成立,求实数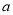 的取值范围;
的取值范围;(3)求证:
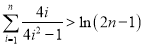 (
(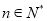 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】学校高一数学考试后,对
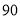 分(含
分(含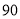 分)以上的成绩进行统计,其頻率分布直方图如图所示,分数在
分)以上的成绩进行统计,其頻率分布直方图如图所示,分数在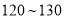 分的学生人数为
分的学生人数为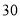 人.
人.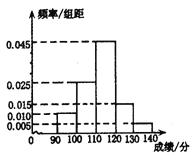
(1)求这所学校分数在
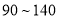 分的学生人数;
分的学生人数;(2)请根据频率发布直方图估计这所学校学生分数在
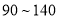 分的学生的平均成绩;
分的学生的平均成绩;(3)为进一步了解学生的学习情况,按分层抽样方法从分数在
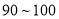 分和
分和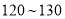 分的学生中抽出
分的学生中抽出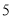 人,从抽出的学生中选出
人,从抽出的学生中选出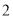 人分别做问卷
人分别做问卷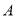 和问卷
和问卷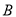 ,求
,求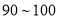 分的学生做问卷
分的学生做问卷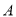 ,
, 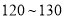 分的学生做问卷
分的学生做问卷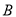 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
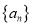 ,
, ,其前
,其前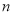 项和
项和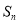 满足
满足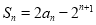 ,其中
,其中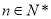 .
.(1)设
 ,证明:数列
,证明:数列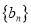 是等差数列;
是等差数列;(2)设
 ,
,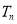 为数列
为数列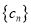 的前
的前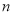 项和,求证:
项和,求证: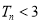 ;
;(3)设
 (
(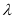 为非零整数,
为非零整数,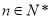 ),试确定
),试确定 的值,使得对任意
的值,使得对任意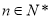 ,都有
,都有 成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在极坐标系中,已知点
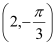 ,圆
,圆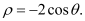
(I)在极坐标系中,以极点为原点,极轴为
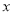 轴正半轴建立平面直角坐标系,取相同的长度单位,求圆
轴正半轴建立平面直角坐标系,取相同的长度单位,求圆 的直角坐标方程;
的直角坐标方程;(II)求点
 到圆
到圆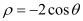 圆心的距离.
圆心的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】先后2次抛掷一枚骰子,将得到的点数分别记为
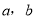 .
.(Ⅰ)求满足
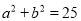 的概率;
的概率;(Ⅱ)设三条线段的长分别为
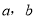 和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
和5,求这三条线段能围成等腰三角形(含等边三角形)的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
 ,
, 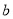 都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;
都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;(2)若
 ,
,  都是从区间
都是从区间 上任取的一个数,求
上任取的一个数,求 成立的概率.
成立的概率.
相关试题

