【题目】先后2次抛掷一枚骰子,将得到的点数分别记为![]() .
.
(Ⅰ)求满足![]() 的概率;
的概率;
(Ⅱ)设三条线段的长分别为![]() 和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:(Ⅰ)首先由a,b的值确定所有基本事件,由![]() 可得到满足条件的点,求其比值可得到概率值;(Ⅱ)由等腰三角形分情况讨论可得到构成三角形的个数,从而求得相应的概率
可得到满足条件的点,求其比值可得到概率值;(Ⅱ)由等腰三角形分情况讨论可得到构成三角形的个数,从而求得相应的概率
试题解析:先后2次抛掷一枚骰子,将得到的点数分别记为![]() 包含的基本事件有:(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),…,(6,5),(6,6),共36个.………………………2分
包含的基本事件有:(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),…,(6,5),(6,6),共36个.………………………2分
(Ⅰ)由于![]() ,
,
∴满足条件的情况只有![]() ,或
,或![]() 两种情况. ……………4分
两种情况. ……………4分
∴满足![]() 的概率为
的概率为![]() . …………………………………………5分
. …………………………………………5分
(Ⅱ)∵三角形的一边长为5,三条线段围成等腰三角形,
∴当![]() 时,
时, ![]() ,共1个基本事件;
,共1个基本事件;
当![]() 时,
时, ![]() ,共1个基本事件;
,共1个基本事件;
当![]() 时,
时, ![]() ,共2个基本事件;
,共2个基本事件;
当![]() 时,
时, ![]() ,共2个基本事件;
,共2个基本事件;
当![]() 时,
时, ![]() ,共6个基本事件;
,共6个基本事件;
当![]() 时,
时, ![]() ,共2个基本事件;
,共2个基本事件;
∴满足条件的基本事件共有1+1+2+2+6+2=14个.…………………………11分
∴三条线段能围成等腰三角形的概率为![]() .…………………………………12分
.…………………………………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
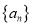 ,
, ,其前
,其前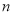 项和
项和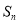 满足
满足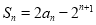 ,其中
,其中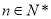 .
.(1)设
 ,证明:数列
,证明:数列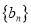 是等差数列;
是等差数列;(2)设
 ,
,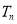 为数列
为数列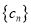 的前
的前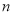 项和,求证:
项和,求证: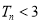 ;
;(3)设
 (
(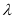 为非零整数,
为非零整数,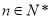 ),试确定
),试确定 的值,使得对任意
的值,使得对任意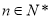 ,都有
,都有 成立.
成立. -
科目: 来源: 题型:
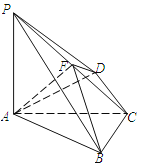
查看答案和解析>>【题目】如图,四棱锥
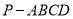 中,
中,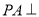 底面
底面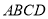 ,
,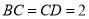 ,
,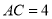 ,
,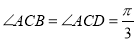 ,
,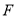 为
为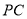 的中点,
的中点,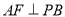 .
.
(1)求
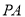 的长;
的长;(2)求二面角
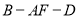 的正弦值.
的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在极坐标系中,已知点
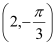 ,圆
,圆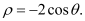
(I)在极坐标系中,以极点为原点,极轴为
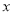 轴正半轴建立平面直角坐标系,取相同的长度单位,求圆
轴正半轴建立平面直角坐标系,取相同的长度单位,求圆 的直角坐标方程;
的直角坐标方程;(II)求点
 到圆
到圆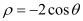 圆心的距离.
圆心的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
 ,
, 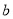 都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;
都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;(2)若
 ,
,  都是从区间
都是从区间 上任取的一个数,求
上任取的一个数,求 成立的概率.
成立的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的方程
的方程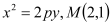 为抛物线
为抛物线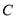 上一点,
上一点,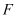 为抛物线的焦点.
为抛物线的焦点.(I)求
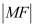 ;
;(II)设直线
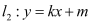 与抛物线
与抛物线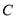 有唯一公共点
有唯一公共点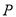 ,且与直线
,且与直线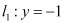 相交于点
相交于点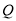 ,试问,在坐标平面内是否存在点
,试问,在坐标平面内是否存在点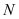 ,使得以
,使得以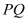 为直径的圆恒过点
为直径的圆恒过点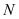 ?若存在,求出点
?若存在,求出点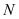 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的图象如图所示.
的图象如图所示.
(Ⅰ)求
 的值;
的值;(Ⅱ)若函数
 在
在 处的切线方程为
处的切线方程为 ,求函数
,求函数 的解析式;
的解析式;(Ⅲ)在(Ⅱ)的条件下,函数
 与
与 的图象有三个不同的交点,求
的图象有三个不同的交点,求 的取值范围.
的取值范围.
相关试题

