【题目】已知数列![]() ,
,![]() ,其前
,其前![]() 项和
项和![]() 满足
满足![]() ,其中
,其中![]() .
.
(1)设![]() ,证明:数列
,证明:数列![]() 是等差数列;
是等差数列;
(2)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证:![]() ;
;
(3)设![]() (
(![]() 为非零整数,
为非零整数,![]() ),试确定
),试确定![]() 的值,使得对任意
的值,使得对任意![]() ,都有
,都有![]() 成立.
成立.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)当![]() 时,
时,![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,整理得:
,整理得:![]() ,可得
,可得![]() ,
,![]() ,
,![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列;(2)由(1)可知:
的等差数列;(2)由(1)可知:![]() ,利用“错位相减法”即可求得
,利用“错位相减法”即可求得![]() ;(3)由
;(3)由![]() 得
得![]() ,整理得:
,整理得:![]() ,当
,当![]() 为奇数时,
为奇数时,![]() ;当
;当![]() 为偶数时,
为偶数时,![]() ,由
,由![]() 为非零整数,即可求得
为非零整数,即可求得![]() .
.
试题解析:(1)当![]() 时,
时,![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() (常数),
(常数),
又![]() ,∴
,∴![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,
的等差数列,![]() .
.
(2)![]() ,
,
![]() ,
,![]() ,
,
相减得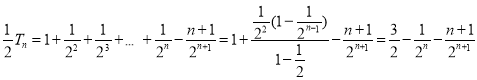 ,
,
∴![]() .
.
(2)由![]() ,得
,得![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
当![]() 为奇数时,
为奇数时,![]() ,∴
,∴![]() ;
;
当![]() 为偶数时,
为偶数时,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又![]() 为非零整数,∴
为非零整数,∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(文科)(本小题满分12分)某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
组号
分组
频数
频率
第一组
[230,235)
8
0.16
第二组
[235,240)
①
0.24
第三组
[240,245)
15
②
第四组
[245,250)
10
0.20
第五组
[250,255]
5
0.10
合 计
50
1.00
(1)写出表中①②位置的数据;
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
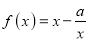 (
(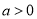 ),
),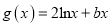 ,且直线
,且直线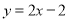 与曲线
与曲线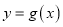 相切.
相切.(1)求
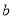 的值;
的值;(2)若对
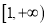 内的一切实数
内的一切实数 ,不等式
,不等式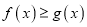 恒成立,求实数
恒成立,求实数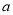 的取值范围;
的取值范围;(3)求证:
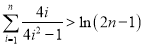 (
(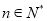 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】学校高一数学考试后,对
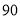 分(含
分(含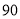 分)以上的成绩进行统计,其頻率分布直方图如图所示,分数在
分)以上的成绩进行统计,其頻率分布直方图如图所示,分数在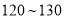 分的学生人数为
分的学生人数为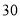 人.
人.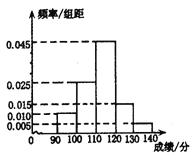
(1)求这所学校分数在
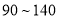 分的学生人数;
分的学生人数;(2)请根据频率发布直方图估计这所学校学生分数在
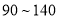 分的学生的平均成绩;
分的学生的平均成绩;(3)为进一步了解学生的学习情况,按分层抽样方法从分数在
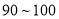 分和
分和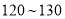 分的学生中抽出
分的学生中抽出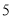 人,从抽出的学生中选出
人,从抽出的学生中选出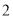 人分别做问卷
人分别做问卷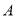 和问卷
和问卷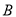 ,求
,求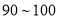 分的学生做问卷
分的学生做问卷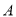 ,
, 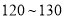 分的学生做问卷
分的学生做问卷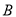 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
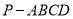 中,
中,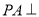 底面
底面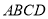 ,
,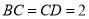 ,
,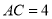 ,
,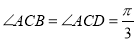 ,
,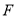 为
为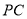 的中点,
的中点,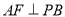 .
.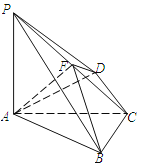
(1)求
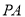 的长;
的长;(2)求二面角
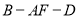 的正弦值.
的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在极坐标系中,已知点
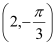 ,圆
,圆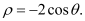
(I)在极坐标系中,以极点为原点,极轴为
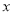 轴正半轴建立平面直角坐标系,取相同的长度单位,求圆
轴正半轴建立平面直角坐标系,取相同的长度单位,求圆 的直角坐标方程;
的直角坐标方程;(II)求点
 到圆
到圆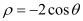 圆心的距离.
圆心的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】先后2次抛掷一枚骰子,将得到的点数分别记为
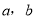 .
.(Ⅰ)求满足
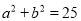 的概率;
的概率;(Ⅱ)设三条线段的长分别为
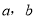 和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
相关试题

