【题目】学校高一数学考试后,对![]() 分(含
分(含![]() 分)以上的成绩进行统计,其頻率分布直方图如图所示,分数在
分)以上的成绩进行统计,其頻率分布直方图如图所示,分数在![]() 分的学生人数为
分的学生人数为![]() 人.
人.
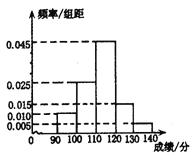
(1)求这所学校分数在![]() 分的学生人数;
分的学生人数;
(2)请根据频率发布直方图估计这所学校学生分数在![]() 分的学生的平均成绩;
分的学生的平均成绩;
(3)为进一步了解学生的学习情况,按分层抽样方法从分数在![]() 分和
分和![]() 分的学生中抽出
分的学生中抽出![]() 人,从抽出的学生中选出
人,从抽出的学生中选出![]() 人分别做问卷
人分别做问卷![]() 和问卷
和问卷![]() ,求
,求![]() 分的学生做问卷
分的学生做问卷![]() ,
, ![]() 分的学生做问卷
分的学生做问卷![]() 的概率.
的概率.
参考答案:
【答案】(1)200人;(2)113分;(3)![]() .
.
【解析】试题分析:(1)由分数在120~130分的学生人数为30人,且分数在120~130分频率为0.15,能求出分数在90~140分的学生人数.
(2)由频率分布直方图能估计这所学校学生分数在90~140分的学生的平均成绩.
(3)分数在90~100分的学生人数为20人,分数在120~130分的学生人数为30人,按照分层抽样方法抽出5人时,从分数在90~100分的学生抽出2人,记为A1,A2,从分数在![]() 分的学生抽出3人,记为B1,B2,B3,从抽取的5人中选出2人分别做问卷A和问卷B,利用列举法能求出90-100分的学生做问卷A,120-130分的学生做问卷B的概率.
分的学生抽出3人,记为B1,B2,B3,从抽取的5人中选出2人分别做问卷A和问卷B,利用列举法能求出90-100分的学生做问卷A,120-130分的学生做问卷B的概率.
试题解析:
(1)![]() 分数在
分数在![]() 分的学生人数为
分的学生人数为![]() 人,且分数在
人,且分数在![]() 分频率为
分频率为![]() ,
, ![]() 分数在
分数在![]() 分的学生人数为
分的学生人数为![]() 人.
人.
(2)估计这所学校学生分数在![]() 分的学生的平均成绩为
分的学生的平均成绩为
![]() 分.
分.
(3)因为分数在![]() 分的学生人数为
分的学生人数为![]() 人,分数在
人,分数在![]() 分的学生人数为
分的学生人数为![]() 人,所以按分层抽样方法抽出
人,所以按分层抽样方法抽出![]() 人时,分数在
人时,分数在![]() 分的学生抽出
分的学生抽出![]() 人,记为
人,记为![]() ,分数在
,分数在![]() 分的学生抽出
分的学生抽出![]() 人,记为
人,记为![]() .从抽出
.从抽出![]() 人中选出
人中选出![]() 人分别做问卷
人分别做问卷![]() 和问卷
和问卷![]() ,共有
,共有![]() 种情况,分别为
种情况,分别为![]() , 设事件
, 设事件![]() “
“![]() 分的学生做问卷
分的学生做问卷![]() ,
, ![]() 分的学生做问卷
分的学生做问卷![]() ”,则事件
”,则事件![]() 共有
共有![]() 种情况,分别为
种情况,分别为![]() ,
, ![]() ,即事件
,即事件![]() 的概率为
的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
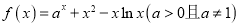 .
.(1)求函数
 在点
在点 处的切线方程;
处的切线方程;(2)求函数
 的单调区间;
的单调区间;(3)若存在
 ,使得
,使得 (
( 是自然对数的底数),求实数
是自然对数的底数),求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(文科)(本小题满分12分)某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
组号
分组
频数
频率
第一组
[230,235)
8
0.16
第二组
[235,240)
①
0.24
第三组
[240,245)
15
②
第四组
[245,250)
10
0.20
第五组
[250,255]
5
0.10
合 计
50
1.00
(1)写出表中①②位置的数据;
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
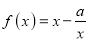 (
(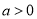 ),
),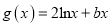 ,且直线
,且直线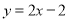 与曲线
与曲线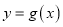 相切.
相切.(1)求
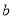 的值;
的值;(2)若对
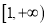 内的一切实数
内的一切实数 ,不等式
,不等式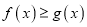 恒成立,求实数
恒成立,求实数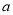 的取值范围;
的取值范围;(3)求证:
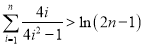 (
(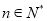 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
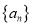 ,
, ,其前
,其前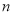 项和
项和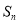 满足
满足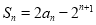 ,其中
,其中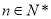 .
.(1)设
 ,证明:数列
,证明:数列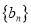 是等差数列;
是等差数列;(2)设
 ,
,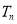 为数列
为数列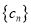 的前
的前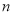 项和,求证:
项和,求证: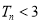 ;
;(3)设
 (
(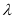 为非零整数,
为非零整数,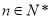 ),试确定
),试确定 的值,使得对任意
的值,使得对任意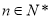 ,都有
,都有 成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
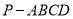 中,
中,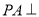 底面
底面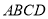 ,
,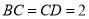 ,
,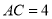 ,
,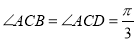 ,
,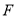 为
为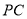 的中点,
的中点,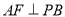 .
.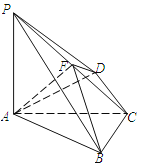
(1)求
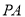 的长;
的长;(2)求二面角
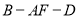 的正弦值.
的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在极坐标系中,已知点
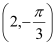 ,圆
,圆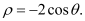
(I)在极坐标系中,以极点为原点,极轴为
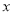 轴正半轴建立平面直角坐标系,取相同的长度单位,求圆
轴正半轴建立平面直角坐标系,取相同的长度单位,求圆 的直角坐标方程;
的直角坐标方程;(II)求点
 到圆
到圆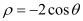 圆心的距离.
圆心的距离.
相关试题

