【题目】已知某班的50名学生进行不记名问卷调查,内容为本周使用手机的时间长,如表:
时间长(小时) |
|
|
|
|
|
女生人数 | 4 | 11 | 3 | 2 | 0 |
男生人数 | 3 | 17 | 6 | 3 | 1 |
(1)求这50名学生本周使用手机的平均时间长;
(2)时间长为![]() 的7名同学中,从中抽取两名,求其中恰有一个女生的概率;
的7名同学中,从中抽取两名,求其中恰有一个女生的概率;
(3)若时间长为![]() 被认定“不依赖手机”,
被认定“不依赖手机”,![]() 被认定“依赖手机”,根据以上数据完成
被认定“依赖手机”,根据以上数据完成![]() 列联表:
列联表:
不依赖手机 | 依赖手机 | 总计 | |
女生 | |||
男生 | |||
总计 |
能否在犯错概率不超过0.15的前提下,认为学生的性别与依赖手机有关系?
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,
,![]() )
)
参考答案:
【答案】(1)9小时;(2)![]() ;(3)答案见解析.
;(3)答案见解析.
【解析】【试题分析】(1)用每组中点值作为代表乘以每组的人数,相加后除以总人数,得到平均时间。(2)利用列举法列出所有的基本事件有![]() 种,其中符合题意的有
种,其中符合题意的有![]() 种,利用古典概型计算公式可求得概率.(3)填写表格后利用公式,计算出
种,利用古典概型计算公式可求得概率.(3)填写表格后利用公式,计算出![]() ,故不能.
,故不能.
【试题解析】
(1)![]() ,
,
所以,这50名学生本周使用手机的平均时间长为9小时.
(2)时间长为![]() 的有7人,记为
的有7人,记为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,其中女生记为
,其中女生记为![]() 、
、![]() 、
、![]() 、
、![]() ,从这7名学生中随机抽取两名的基本事件有:
,从这7名学生中随机抽取两名的基本事件有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共21个.
共21个.
设事件![]() 表示恰有一位女生符合要求的事件有:
表示恰有一位女生符合要求的事件有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共12个.
共12个.
所以恰有一个女生的概率为![]() .
.
(3)
依赖手机 | 总计 | ||
女生 | 15 | 5 | 20 |
男生 | 20 | 10 | 30 |
总计 | 35 | 15 | 50 |
![]() ,
,
不能在犯错概率不超过0.15的前提下,认为学生的性别与依赖手机有关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形
 中,
中, ,
, ,
, ,
, ,四边形
,四边形 是菱形,
是菱形, .
.(Ⅰ)求证:
 ;
;(Ⅱ)求二面角
 的平面角的正切值.
的平面角的正切值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 上的点到椭圆一个焦点的距离的最大值是最小值的
上的点到椭圆一个焦点的距离的最大值是最小值的 倍,且点
倍,且点 在椭圆
在椭圆 上.
上.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)过点
 任作一条直线
任作一条直线 ,
, 与椭圆
与椭圆 交于不同于
交于不同于 点的
点的 、
、 两点,
两点, 与直线
与直线 交于
交于 点,记直线
点,记直线 、
、 、
、 的斜率分别为
的斜率分别为 、
、 、
、 .试探究
.试探究 与
与 的关系,并证明你的结论.
的关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018湖南(长郡中学、株洲市第二中学)、江西(九江一中)等十四校高三第一次联考】已知函数
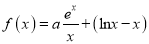 (其中
(其中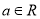 且
且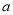 为常数,
为常数, 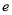 为自然对数的底数,
为自然对数的底数, 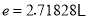 ).
).(Ⅰ)若函数
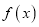 的极值点只有一个,求实数
的极值点只有一个,求实数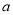 的取值范围;
的取值范围;(Ⅱ)当
 时,若
时,若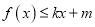 (其中
(其中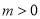 )恒成立,求
)恒成立,求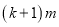 的最小值
的最小值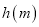 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】以原点
 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线 的极坐标方程为:
的极坐标方程为: ,在平面直角坐标系
,在平面直角坐标系 中,直线
中,直线 的方程为
的方程为 (
( 为参数).
为参数).(1)求曲线
 和直线
和直线 的直角坐标方程;
的直角坐标方程;(2)已知直线
 交曲线
交曲线 于
于 ,
, 两点,求
两点,求 ,
, 两点的距离.
两点的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
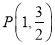 在椭圆
在椭圆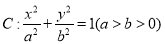 上,
上, 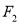 为椭圆
为椭圆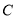 的右焦点,
的右焦点, 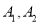 分别为椭圆
分别为椭圆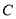 的左,右两个顶点.若过点
的左,右两个顶点.若过点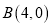 且斜率不为0的直线
且斜率不为0的直线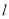 与椭圆
与椭圆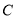 交于
交于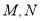 两点,且线段
两点,且线段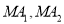 的斜率之积为
的斜率之积为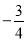 .
.(1)求椭圆
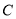 的方程;
的方程;(2)已知直线
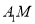 与
与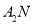 相交于点
相交于点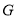 ,证明:
,证明: 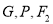 三点共线.
三点共线. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若函数
 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;(2)若函数
 在
在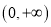 上存在两个极值点
上存在两个极值点 ,且
,且 ,证明:
,证明:  .
.
相关试题

