【题目】已知函数![]()
(I)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(Ⅱ)若函数![]() 在
在![]() 上单调递增,试求出
上单调递增,试求出![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() 和
和![]() .(Ⅱ)
.(Ⅱ) ![]() .
.
【解析】试题分析:(1)先求导数,再求导函数零点,列表分析导函数符号变化规律,最后根据导函数符号确定单调区间,(2)由题意得![]() 在区间
在区间![]() 恒成立,再变量分离得
恒成立,再变量分离得![]() ,最后根据二次函数性质求最值,得
,最后根据二次函数性质求最值,得![]() 的取值范围.
的取值范围.
试题解析:(I)当![]() 时,函数
时,函数![]()
![]()
令![]() 即
即![]() 解得
解得![]()
令![]() 解得
解得![]() 或
或![]()
所以当![]() 时,函数
时,函数![]() 的单调递增区间是
的单调递增区间是![]() ,
,
单调递减区间是![]() 和
和![]() .
.
(Ⅱ)法一: ![]()
函数![]() 在
在![]() 上单调递增,
上单调递增,
等价于![]() 在区间
在区间![]() 恒成立,
恒成立,
等价于![]() 在区间
在区间![]() 恒成立.
恒成立.
等价于![]()
令![]()
因为![]()
所以函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
故![]()
所以![]() 的取值范围是
的取值范围是![]()
法二: ![]()
函数![]() 在
在![]() 上单调递增,
上单调递增,
等价于![]() 在区间
在区间![]() 恒成立,
恒成立,
令![]()
则命题等价于![]() 在区间
在区间![]() 恒成立.
恒成立.
当![]() 时,由
时,由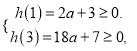 解得
解得![]()
当![]() 时因为函数图像的对称轴
时因为函数图像的对称轴![]()
此时只有满足![]() ,解得
,解得![]() .
.
综上所述![]() 的取值范围是
的取值范围是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1.
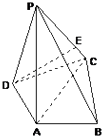
(1)求二面角A﹣PB﹣C的余弦值.
(2)在线段CP上是否存在一点E,使得DE⊥PB,若存在,求线段CE的长度,不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
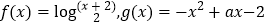
(1)判断函数
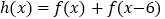 的单调性,并说明理由
的单调性,并说明理由(2)若对任意的
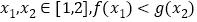 恒成立,求a的取值范围
恒成立,求a的取值范围 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)若函数
 恰有两个不相同的零点,求实数
恰有两个不相同的零点,求实数 的值;
的值;(2)记
 为函数
为函数 的所有零点之和,当
的所有零点之和,当 时,求
时,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
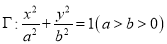 的左、右焦点分别是
的左、右焦点分别是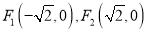 ,且点
,且点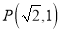 在
在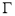 上,抛物线
上,抛物线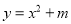 与椭圆
与椭圆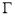 交于四点
交于四点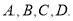
(I)求
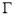 的方程;
的方程;(Ⅱ)试探究坐标平面上是否存在定点
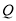 ,满足
,满足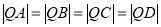 ?(若存在,求出
?(若存在,求出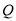 的坐标;若不存在,需说明理由.)
的坐标;若不存在,需说明理由.) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
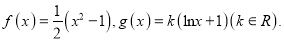
(Ⅰ)若
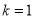 ,求
,求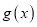 在
在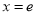 处的切线方程;
处的切线方程;(Ⅱ)证明:对任意正数
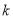 ,函数
,函数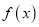 和
和 的图像总有两个公共点.
的图像总有两个公共点. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正三棱柱
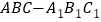 的高为2,
的高为2,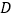 是
是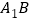 的中点,
的中点,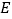 是
是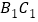 的中点
的中点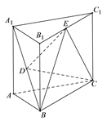
(1)证明:
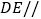 平面
平面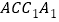 ;
;(2)若三棱锥
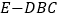 的体积为
的体积为 ,求该正三棱柱的底面边长.
,求该正三棱柱的底面边长.
相关试题

