【题目】已知函数![]()
(Ⅰ)若![]() ,求
,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)证明:对任意正数![]() ,函数
,函数![]() 和
和![]() 的图像总有两个公共点.
的图像总有两个公共点.
参考答案:
【答案】(Ⅰ) ![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】试题分析:(I)先根据导数几何意义得切线的斜率![]() ,再根据点斜式得切线方程;(Ⅱ)函数
,再根据点斜式得切线方程;(Ⅱ)函数![]() 和
和![]() 的图像总有两个公共点,等价于
的图像总有两个公共点,等价于![]()
![]() 总有两个实数根.变量分离得
总有两个实数根.变量分离得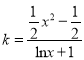 ,再根据导数研究函数
,再根据导数研究函数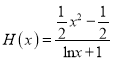 单调性,结合图像确定有两个交点的条件,即得证.
单调性,结合图像确定有两个交点的条件,即得证.
试题解析:(I)![]() 时,则
时,则![]()
![]() 在
在![]() 处的切线的斜率
处的切线的斜率![]()
又![]() 时,
时, ![]() 即切点
即切点![]() ,
,
所以![]() 在
在![]() 处的切线方程为:
处的切线方程为:
![]() ,即
,即![]()
(Ⅱ)法一:
记![]()
则![]() (已知
(已知![]() ).
).
因为![]() 有意义,
有意义, ![]()
所以![]()
所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
故![]()
记![]()
![]()
因为![]()
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
故![]()
故![]() 恒成立,即
恒成立,即![]()
又![]() 时,
时, ![]() 时,
时, ![]() ,
,
故![]() 在
在![]() 和
和![]() 各有一个零点,
各有一个零点,
即![]() 和
和![]() 的图像在
的图像在![]() 和
和![]() 各有且只有一个公共点.
各有且只有一个公共点.
法二:函数![]() 和
和![]() 的图像总有两个公共点,等价于
的图像总有两个公共点,等价于![]()
![]() 总有两个实数根.
总有两个实数根.
![]()
![]() 显示
显示![]() 不是该方程的根.
不是该方程的根.
当![]() 时,
时, 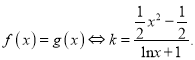
记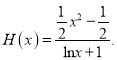
则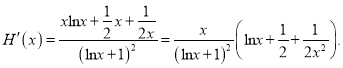
再记![]()
因为![]()
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减
单调递减
所以![]()
即![]()
从而![]() 在
在![]() 和
和![]() 均单调递增,
均单调递增,
又![]() 时,
时, ![]() 时,
时, ![]() 时,
时, ![]() ,
,
又![]() 时,
时, ![]() 时,
时, ![]() 时,
时, ![]() ,
,
![]() 的草图如图:
的草图如图:
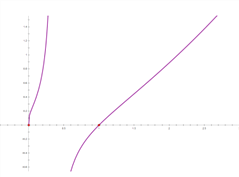
故对任意的正数![]() ,直线
,直线![]() 与
与![]() 的图像总有两个公共点,
的图像总有两个公共点,
即方程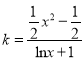 总有两个根,
总有两个根,
即函数![]() 和
和![]() 的图像总有两个公共点,命题得证.
的图像总有两个公共点,命题得证.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)若函数
 恰有两个不相同的零点,求实数
恰有两个不相同的零点,求实数 的值;
的值;(2)记
 为函数
为函数 的所有零点之和,当
的所有零点之和,当 时,求
时,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
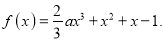
(I)当
 时,求
时,求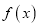 的单调区间;
的单调区间;(Ⅱ)若函数
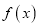 在
在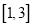 上单调递增,试求出
上单调递增,试求出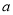 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
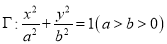 的左、右焦点分别是
的左、右焦点分别是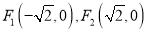 ,且点
,且点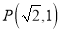 在
在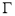 上,抛物线
上,抛物线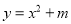 与椭圆
与椭圆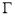 交于四点
交于四点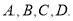
(I)求
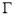 的方程;
的方程;(Ⅱ)试探究坐标平面上是否存在定点
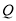 ,满足
,满足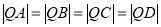 ?(若存在,求出
?(若存在,求出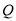 的坐标;若不存在,需说明理由.)
的坐标;若不存在,需说明理由.) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正三棱柱
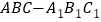 的高为2,
的高为2,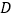 是
是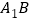 的中点,
的中点,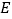 是
是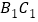 的中点
的中点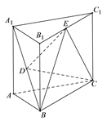
(1)证明:
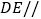 平面
平面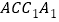 ;
;(2)若三棱锥
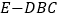 的体积为
的体积为 ,求该正三棱柱的底面边长.
,求该正三棱柱的底面边长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
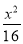 +
+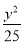 =1的焦点分别是
=1的焦点分别是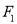 、
、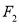 ,
, 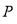 是椭圆上一点,若连结
是椭圆上一点,若连结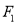 、
、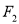 、
、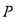 三点恰好能构成直角三角形,则点
三点恰好能构成直角三角形,则点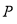 到
到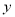 轴的距离是( )
轴的距离是( )A.
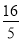 B.
B. 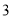 C.
C. 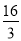 D.
D. 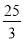
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 是定义在
是定义在 上的偶函数,且对任意的
上的偶函数,且对任意的 恒有
恒有 ,已知当
,已知当 时,
时, ,则下列命题:
,则下列命题:①对任意
 ,都有
,都有 ;②函数
;②函数 在
在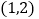 上递减,在
上递减,在 上递增;
上递增;③函数
 的最大值是1,最小值是0;④当
的最大值是1,最小值是0;④当 时,
时, .
.其中正确命题的序号有________.
相关试题

