【题目】某校200名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这200名学生的平均分;
(3)若这200名学生的数学成绩中,某些分数段的人数![]() 与英语成绩相应分数段的人数
与英语成绩相应分数段的人数![]() 之比如下表所示,求英语成绩在
之比如下表所示,求英语成绩在![]() 的人数.
的人数.
分数段 |
|
|
|
|
|
| 1:2 | 2:1 | 6:5 | 1:2 | 1:1 |
参考答案:
【答案】(1)![]() (2)
(2)![]() 分(3)140人
分(3)140人
【解析】
(1)在频率分布直方图中所有小矩形的面积之和为1,由此可得![]() ;
;
(2)频率分布直方图中每一个小矩形的面积乘以底边中点的横坐标之和即为平均数,即为估计平均数;
(3)求出这200名学生的数学成绩在![]() ,
,![]() ,
,![]() 的人数,然后计算出各分数段的英语人数即可.
的人数,然后计算出各分数段的英语人数即可.
(1)由![]() ,解得
,解得![]() .
.
(2)频率分布直方图中每一个小矩形的面积乘以底边中点的横坐标之和即为平均数,即估计平均数为
![]() .
.
(3)由频率分布直方图可求出这200名学生的数学成绩在![]() ,
,![]() ,
,![]() 的分别有60人,40人,10人,按照表中给的比例,则英语成绩在
的分别有60人,40人,10人,按照表中给的比例,则英语成绩在![]() ,
,![]() ,
,![]() 的分别有50人,80人,10人,所以英语成绩在
的分别有50人,80人,10人,所以英语成绩在![]() 的有140人.
的有140人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(1)若
 ,求函数
,求函数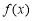 的零点;
的零点;(2)若
 在
在 恒成立,求
恒成立,求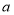 的取值范围;
的取值范围;(3)设函数
 ,解不等式
,解不等式 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b=acosC+3bsin(B+C).
(1)若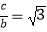 ,求角A;
,求角A;
(2)在(1)的条件下,若△ABC的面积为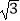 ,求a的值.
,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
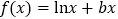 .
.(Ⅰ)当
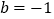 时,求函数
时,求函数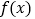 的单调区间;
的单调区间;(Ⅱ)当
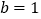 时,
时,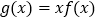 对任意
对任意 恒在函数
恒在函数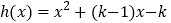 上方,若
上方,若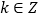 ,求
,求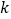 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若如下框图所给的程序运行结果为
 ,那么判断框中应填入的关于
,那么判断框中应填入的关于 的条件是( )
的条件是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某销售公司拟招聘一名产品推销员,有如下两种工资方案:
方案一:每月底薪2000元,每销售一件产品提成15元;
方案二:每月底薪3500元,月销售量不超过300件,没有提成,超过300件的部分每件提成30元.
(1)分别写出两种方案中推销员的月工资
 (单位:元)与月销售产品件数
(单位:元)与月销售产品件数 的函数关系式;
的函数关系式;(2)从该销售公司随机选取一名推销员,对他(或她)过去两年的销售情况进行统计,得到如下统计表:
月销售产品件数

300
400
500
600
700
次数
2
4
9
5
4
把频率视为概率,分别求两种方案推销员的月工资超过11090元的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班在一次个人投篮比赛中,记录了在规定时间内投进
 个球的人数分布情况:
个球的人数分布情况:进球数
 (个)
(个)0
1
2
3
4
5
投进
 个球的人数(人)
个球的人数(人)1
2
7
2
其中
 和
和 对应的数据不小心丢失了,已知进球3个或3个以上,人均投进4个球;进球5个或5个以下,人均投进2.5个球.
对应的数据不小心丢失了,已知进球3个或3个以上,人均投进4个球;进球5个或5个以下,人均投进2.5个球.(1)投进3个球和4个球的分别有多少人?
(2)从进球数为3,4,5的所有人中任取2人,求这2人进球数之和为8的概率.
相关试题

