【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,
时,![]() 对任意
对任意![]() 恒在函数
恒在函数![]() 上方,若
上方,若![]() ,求
,求![]() 的最大值.
的最大值.
参考答案:
【答案】(1)![]() 在
在![]() 单调递增, 在
单调递增, 在![]() 单调递减;(2)
单调递减;(2)![]() .
.
【解析】分析:(1)求出导函数![]() ,解不等式
,解不等式![]() 得增区间,解不等式
得增区间,解不等式![]() 得减区间;
得减区间;
(2)令![]() ,求出导函数
,求出导函数![]() ,可按
,可按![]() 和
和![]() 分类讨论
分类讨论![]() 的正负,确定
的正负,确定![]() 的单调性,得出
的单调性,得出![]() 的最小值,由最小值>0得
的最小值,由最小值>0得![]() 的满园.
的满园.
详解:(1)![]() 在
在![]() 单调递增, 在
单调递增, 在![]() 单调递减.
单调递减.
(2)法一:令![]() , 则
, 则![]() , ①当
, ①当![]() 即
即![]() 时,
时,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上单调递增,又
上单调递增,又![]() 所
所![]() ,
,![]() ,
,![]() ;
;
②当![]() 即
即![]() 时,令
时,令![]() ,得
,得![]()
![]() 时,
时,![]() ,则
,则![]() 单调递减;
单调递减;
![]() 时,
时,![]() ,则
,则![]() 单调递增.
单调递增.
故![]() ,令
,令![]() ,
,
则![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,
,![]()
![]() ,
,![]() .
.
综上所述,![]() .
.
法二:![]() ,
,![]() 恒在
恒在![]() 上方,即
上方,即![]() ,
,![]() 恒成立.
恒成立.
即![]() 恒成立,也即:
恒成立,也即:![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,则
,则![]()
令![]() ,则
,则![]() ,
,
故![]() 在
在![]() 上单调递增,而
上单调递增,而![]()
所以![]() 存在唯一的零点
存在唯一的零点![]() ,即
,即![]()
当![]() ,
,![]() 单调递减;
单调递减;![]() 单调递增
单调递增 ![]()
即![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣2|﹣|x+1|.
(1)解不等式f(x)>1.
(2)当x>0时,函数g(x)= (a>0)的最小值总大于函数f(x),试求实数a的取值范围.
(a>0)的最小值总大于函数f(x),试求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(1)若
 ,求函数
,求函数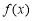 的零点;
的零点;(2)若
 在
在 恒成立,求
恒成立,求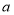 的取值范围;
的取值范围;(3)设函数
 ,解不等式
,解不等式 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b=acosC+3bsin(B+C).
(1)若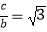 ,求角A;
,求角A;
(2)在(1)的条件下,若△ABC的面积为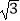 ,求a的值.
,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校200名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是
 ,
, ,
, ,
, ,
, .
.
(1)求图中
 的值;
的值;(2)根据频率分布直方图,估计这200名学生的平均分;
(3)若这200名学生的数学成绩中,某些分数段的人数
 与英语成绩相应分数段的人数
与英语成绩相应分数段的人数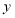 之比如下表所示,求英语成绩在
之比如下表所示,求英语成绩在 的人数.
的人数.分数段






1:2
2:1
6:5
1:2
1:1
-
科目: 来源: 题型:
查看答案和解析>>【题目】若如下框图所给的程序运行结果为
 ,那么判断框中应填入的关于
,那么判断框中应填入的关于 的条件是( )
的条件是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某销售公司拟招聘一名产品推销员,有如下两种工资方案:
方案一:每月底薪2000元,每销售一件产品提成15元;
方案二:每月底薪3500元,月销售量不超过300件,没有提成,超过300件的部分每件提成30元.
(1)分别写出两种方案中推销员的月工资
 (单位:元)与月销售产品件数
(单位:元)与月销售产品件数 的函数关系式;
的函数关系式;(2)从该销售公司随机选取一名推销员,对他(或她)过去两年的销售情况进行统计,得到如下统计表:
月销售产品件数

300
400
500
600
700
次数
2
4
9
5
4
把频率视为概率,分别求两种方案推销员的月工资超过11090元的概率.
相关试题

