【题目】已知函数![]()
(1)若![]() ,求函数
,求函数![]() 的零点;
的零点;
(2)若![]() 在
在![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)设函数![]() ,解不等式
,解不等式![]() .
.
参考答案:
【答案】(1)1;(2) ![]() (3)见解析
(3)见解析
【解析】
(1)解方程![]() 可得零点;
可得零点;
(2)![]() 恒成立,可分离参数得
恒成立,可分离参数得![]() ,这样只要求得
,这样只要求得![]() 在
在![]() 上的最大值即可;
上的最大值即可;
(3)注意到![]() 的定义域,不等式
的定义域,不等式![]() 等价于
等价于![]() ,这样可根据
,这样可根据![]() 与0,1的大小关系分类讨论.
与0,1的大小关系分类讨论.
(1)当![]() 时,
时,![]()
令![]() 得,
得,![]() ,∵
,∵![]() ,∴函数
,∴函数![]() 的零点是1
的零点是1
(2)![]()
![]() 在
在![]() 恒成立,即
恒成立,即![]() 在
在![]() 恒成立,
恒成立,
分离参数得:![]() ,
,
∵![]() ,∴
,∴![]()
从而有:![]() .
.
(3)![]()
令![]() ,得
,得![]() ,
,![]() ,
,
因为函数![]() 的定义域为
的定义域为![]() ,所以
,所以![]() 等价于
等价于![]()
(1)当![]() ,即
,即![]() 时,
时,![]() 恒成立,
恒成立,![]() 原不等式的解集是
原不等式的解集是![]()
(2)当![]() ,即
,即![]() 时,
时,![]() 原不等式的解集是
原不等式的解集是![]()
(3)当![]() ,即
,即![]() 时,
时,![]() 原不等式的解集是
原不等式的解集是![]()
(4)当![]() ,即
,即![]() 时,
时,![]() 原不等式的解集是
原不等式的解集是![]()
综上所述:当![]() 时,
时,![]() 原不等式的解集是
原不等式的解集是![]()
当![]() 时,
时,![]() 原不等式的解集是
原不等式的解集是![]()
当![]() 时,
时,![]() 原不等式的解集是
原不等式的解集是![]()
当![]() 时,
时,![]() 原不等式的解集是
原不等式的解集是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的非负半轴重合,若曲线C1的方程为ρsin(θ+
 )+2
)+2  =0,曲线C2的参数方程为
=0,曲线C2的参数方程为  (θ为参数).
(θ为参数).
(1)将C1的方程化为直角坐标方程;
(2)若点Q为C2上的动点,P为C1上的动点,求|PQ|的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年04月13日“山东济南非法经营疫苗系列案件”披露后,引发社会高度关注,引起公众、受种者和儿童家长对涉案疫苗安全性和有效性的担忧。为采取后续处置措施提供依据,保障受种者的健康,尽快恢复公众接种疫苗的信心,科学严谨地分析涉案疫苗接种给受种者带来的安全性风险和是否有效,对某疫苗预防疾病的效果,进行动物实验,得到下面表格中的统计数据:现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为
 .
.未发病
发病
合计
未注射疫苗



注射疫苗



合计



(1)求
 列联表中的数据
列联表中的数据 的值;
的值;(2)绘制发病率的条形统计图,并判断疫苗是否有效?











(3)能够有多大把握认为疫苗有效?
附:

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣2|﹣|x+1|.
(1)解不等式f(x)>1.
(2)当x>0时,函数g(x)= (a>0)的最小值总大于函数f(x),试求实数a的取值范围.
(a>0)的最小值总大于函数f(x),试求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b=acosC+3bsin(B+C).
(1)若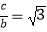 ,求角A;
,求角A;
(2)在(1)的条件下,若△ABC的面积为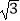 ,求a的值.
,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
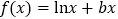 .
.(Ⅰ)当
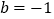 时,求函数
时,求函数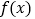 的单调区间;
的单调区间;(Ⅱ)当
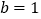 时,
时,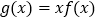 对任意
对任意 恒在函数
恒在函数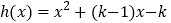 上方,若
上方,若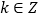 ,求
,求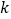 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校200名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是
 ,
, ,
, ,
, ,
, .
.
(1)求图中
 的值;
的值;(2)根据频率分布直方图,估计这200名学生的平均分;
(3)若这200名学生的数学成绩中,某些分数段的人数
 与英语成绩相应分数段的人数
与英语成绩相应分数段的人数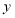 之比如下表所示,求英语成绩在
之比如下表所示,求英语成绩在 的人数.
的人数.分数段






1:2
2:1
6:5
1:2
1:1
相关试题

