【题目】口袋中装有2个白球和n(n≥2,n![]() N*)个红球.每次从袋中摸出2个球(每次摸球后把这2个球放回口袋中),若摸出的2个球颜色相同则为中奖,否则为不中奖.
N*)个红球.每次从袋中摸出2个球(每次摸球后把这2个球放回口袋中),若摸出的2个球颜色相同则为中奖,否则为不中奖.
(I)用含n的代数式表示1次摸球中奖的概率;
(Ⅱ)若n=3,求3次摸球中恰有1次中奖的概率;
(III)记3次摸球中恰有1次中奖的概率为f(p),当f(p)取得最大值时,求n的值.
参考答案:
【答案】(I)![]() ;(II)
;(II)![]() ;(III)当f(p)取得最大值时,n的值为2.
;(III)当f(p)取得最大值时,n的值为2.
【解析】试题分析:
(1)由题意结合古典概型公式可得所求概率值为![]() ;
;
(2)利用二项分布可得3次摸球中恰有1次中奖的概率是![]() ;
;
(3)结合概率函数的解析式可得当f(p)取得最大值时,n的值为2.
试题解析:
(I)设“1次摸球中奖”为事件A,则P(A)=![]() ,
,
(II)由(I)得,若n=3,则1次摸球中奖的概率为p=![]() =
=![]() =
=![]() ,
,
所以3次摸球中,恰有1次中奖的概率为P3(1)=![]() ,
,
(III)设“1次摸球中奖”的概率为p,
则3次摸球中,恰有1次中奖的概率为
f(p)=C![]() p(1-p)2 =3p3-6p2+3p(0<p<1),
p(1-p)2 =3p3-6p2+3p(0<p<1),
因为f'(p)=9p2-12p+3=3(p-1)(3p-1),
所以,当p∈(0, ![]() )时,f(p)单调递增;当p∈(
)时,f(p)单调递增;当p∈(![]() ,1)时,f(p)单调递减,
,1)时,f(p)单调递减,
所以,当p=![]() 时,f(p)取得最大值.
时,f(p)取得最大值.
令![]() ,解得n=2,n=1(舍去).
,解得n=2,n=1(舍去).
所以,当f(p)取得最大值时,n的值为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】幂函数f(x)=x3m-5(m∈N)在(0,+∞)上是减函数,且f(-x)=f(x),则m可能等于( )
A. 0 B. 1
C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
 上的函数
上的函数  和
和 的图象如图
的图象如图

给出下列四个命题:
①方程
 有且仅有
有且仅有 个根;②方程
个根;②方程 有且仅有
有且仅有 个根;
个根;③方程
 有且仅有
有且仅有 个根;④方程
个根;④方程 有且仅有
有且仅有 个根;
个根;其中正确命题的序号是( )
A. ①②③ B. ②③④ C. ①②④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
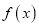 是定义在区间
是定义在区间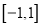 上的奇函数,且
上的奇函数,且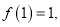 若对于任意的
若对于任意的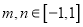 有
有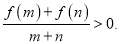
(1)判断并证明函数的单调性;
(2)解不等式
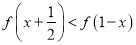 ;
;(3)若
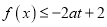 对于任意的
对于任意的 ,
, 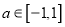 恒成立,求实数
恒成立,求实数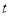 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
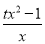
 (t+1)lnx,,其中t∈R.
(t+1)lnx,,其中t∈R.(1)若t=1,求证:当x>1时,f(x)>0成立;
(2)若t>
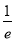 ,判断函数g(x)=x[f(x)+t+1]的零点的个数.
,判断函数g(x)=x[f(x)+t+1]的零点的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
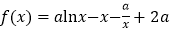 (其中
(其中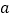 为常数,
为常数,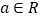 ).(Ⅰ)求函数
).(Ⅰ)求函数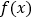 的单调区间;(Ⅱ)当
的单调区间;(Ⅱ)当 时,是否存在实数
时,是否存在实数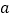 ,使得当
,使得当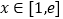 时,不等式
时,不等式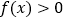 恒成立?如果存在,求
恒成立?如果存在,求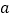 的取值范围;如果不存在,请说明理由(其中
的取值范围;如果不存在,请说明理由(其中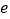 是自然对数的底数,
是自然对数的底数,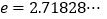 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,且
,且 .
.(1)判断函数
 的奇偶性;
的奇偶性;(2) 判断函数
 在(1,+∞)上的单调性,并用定义证明你的结论;
在(1,+∞)上的单调性,并用定义证明你的结论;(3)若
 ,求实数a的取值范围.
,求实数a的取值范围.
相关试题

