【题目】已知函数f(x)=![]()
![]() (t+1)lnx,,其中t∈R.
(t+1)lnx,,其中t∈R.
(1)若t=1,求证:当x>1时,f(x)>0成立;
(2)若t>![]() ,判断函数g(x)=x[f(x)+t+1]的零点的个数.
,判断函数g(x)=x[f(x)+t+1]的零点的个数.
参考答案:
【答案】(1)见解析(2)1
【解析】试题分析:(1)当![]() 时,对
时,对![]() 求导,
求导, ![]() 得增区间,
得增区间, ![]() 得减区间,进而求出函数的最小值值,即可证明;(2)若t>
得减区间,进而求出函数的最小值值,即可证明;(2)若t>![]() ,求得函数g(x)=x[f(x)+t+1]的导函数,研究其单调性,根据零点定理再利用导数即可判定零点的个数.
,求得函数g(x)=x[f(x)+t+1]的导函数,研究其单调性,根据零点定理再利用导数即可判定零点的个数.
试题解析:解:(1)t=1时,f(x)=x﹣![]() ﹣2lnx,x>0
﹣2lnx,x>0
∴f′(x)=1+![]() ﹣
﹣![]() =
=![]() =
=![]() ≥0,
≥0,
∴f(x)在(1,+∞)上单调递增,
∴f(x)>f(1)=1﹣1﹣0=0,
∴x>1,f(x)>0成立,
(2)当x∈(0,+∞),g(x)=tx2﹣(t+1)xlnx+(t+1)x﹣1
∴g′(x)=2tx﹣(t+1)lnx,
设m(x)=2tx﹣(t+1)lnx, ∴m′(x)=2t﹣![]() =
=![]() ,
,
令m′(x)=0,得x=![]() ,
,
当0<x<![]() 时,m'(x)<0;当时x>
时,m'(x)<0;当时x>![]() ,m'(x)>0.
,m'(x)>0.
∴g'(x)在(0,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增.
,+∞)上单调递增.
∴g'(x)的最小值为g′(![]() )=(t+1)(1﹣ln
)=(t+1)(1﹣ln![]() ),
),
∵t>![]() ,∴
,∴![]() =
=![]() +
+![]() <
<![]() +
+![]() <e.
<e.
∴g'(x)的最小值g′(![]() )=(t+1)(1﹣ln
)=(t+1)(1﹣ln![]() )>0,
)>0,
从而,g(x)在区间(0,+∞)上单调递增.
又g(1)=2t>0,又g(![]() )=
)=![]() +
+![]() (6+2lnt)﹣1,
(6+2lnt)﹣1,
设h(t)=e3t﹣(2lnt+6).
则h′(t)=e3﹣![]() .
.
令h'(t)=0得t=![]() .由h'(t)<0,得0<t<
.由h'(t)<0,得0<t<![]() ;
;
由h'(t)>0,得t>![]() .
.
∴h(t)在(0,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增.
,+∞)上单调递增.
∴h(t)min=h(![]() )=2﹣2ln2>0.
)=2﹣2ln2>0.
∴h(t)>0恒成立.∴e3t>2lnt+6,.
∴g(![]() )<
)<![]() +
+![]() ﹣1=
﹣1=![]() +
+![]() +
+![]() ﹣1<
﹣1<![]() +
+![]() +
+![]() ﹣1<0.
﹣1<0.
∴当t>![]() 时,函数g(x)恰有1个零点
时,函数g(x)恰有1个零点
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
 上的函数
上的函数  和
和 的图象如图
的图象如图

给出下列四个命题:
①方程
 有且仅有
有且仅有 个根;②方程
个根;②方程 有且仅有
有且仅有 个根;
个根;③方程
 有且仅有
有且仅有 个根;④方程
个根;④方程 有且仅有
有且仅有 个根;
个根;其中正确命题的序号是( )
A. ①②③ B. ②③④ C. ①②④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
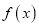 是定义在区间
是定义在区间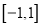 上的奇函数,且
上的奇函数,且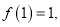 若对于任意的
若对于任意的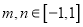 有
有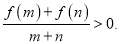
(1)判断并证明函数的单调性;
(2)解不等式
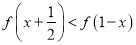 ;
;(3)若
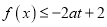 对于任意的
对于任意的 ,
, 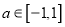 恒成立,求实数
恒成立,求实数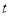 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】口袋中装有2个白球和n(n≥2,n
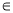 N*)个红球.每次从袋中摸出2个球(每次摸球后把这2个球放回口袋中),若摸出的2个球颜色相同则为中奖,否则为不中奖.
N*)个红球.每次从袋中摸出2个球(每次摸球后把这2个球放回口袋中),若摸出的2个球颜色相同则为中奖,否则为不中奖.(I)用含n的代数式表示1次摸球中奖的概率;
(Ⅱ)若n=3,求3次摸球中恰有1次中奖的概率;
(III)记3次摸球中恰有1次中奖的概率为f(p),当f(p)取得最大值时,求n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
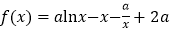 (其中
(其中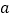 为常数,
为常数,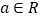 ).(Ⅰ)求函数
).(Ⅰ)求函数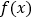 的单调区间;(Ⅱ)当
的单调区间;(Ⅱ)当 时,是否存在实数
时,是否存在实数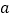 ,使得当
,使得当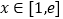 时,不等式
时,不等式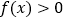 恒成立?如果存在,求
恒成立?如果存在,求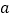 的取值范围;如果不存在,请说明理由(其中
的取值范围;如果不存在,请说明理由(其中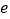 是自然对数的底数,
是自然对数的底数,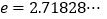 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,且
,且 .
.(1)判断函数
 的奇偶性;
的奇偶性;(2) 判断函数
 在(1,+∞)上的单调性,并用定义证明你的结论;
在(1,+∞)上的单调性,并用定义证明你的结论;(3)若
 ,求实数a的取值范围.
,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】中石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分儿口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探. 由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用.勘探初期数据资料见如表:

(Ⅰ)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为
 ,求
,求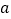 ,并估计
,并估计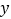 的预报值;
的预报值; (Ⅱ)现准备勘探新井
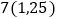 ,若通过1、3、5、7号井计算出的
,若通过1、3、5、7号井计算出的 的值(
的值( 精确到0.01)相比于(Ⅰ)中
精确到0.01)相比于(Ⅰ)中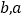 的值之差不超过10%,则使用位置最接近的已有旧井
的值之差不超过10%,则使用位置最接近的已有旧井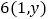 ,否则在新位置打开,请判断可否使用旧井?
,否则在新位置打开,请判断可否使用旧井?(参考公式和计算结果:
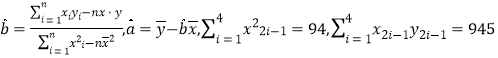 )
)(Ⅲ)设出油量与勘探深度的比值
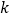 不低于20的勘探并称为优质井,那么在原有井号1~6的出油量不低于50L的井中任意勘探3口井,求恰好2口是优质井的概率.
不低于20的勘探并称为优质井,那么在原有井号1~6的出油量不低于50L的井中任意勘探3口井,求恰好2口是优质井的概率.
相关试题

