【题目】某小组共10人,利用假期参加义工活动,已知参加义工活动1次的有2人,2次的有4人,3次的有4人.现从这10人中随机选出2人作为该组代表参加座谈会.
(1)设![]() 为事件“选出的2人参加义工活动次数之和为4”,求事件
为事件“选出的2人参加义工活动次数之和为4”,求事件![]() 发生的概率;
发生的概率;
(2)设![]() 为选出的2人参加义工活动次数之差的绝对值,求随机变量
为选出的2人参加义工活动次数之差的绝对值,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
参考答案:
【答案】(1)![]() .(2)见解析.
.(2)见解析.
【解析】试题分析:(1)由已知得![]() ,即可得到事件
,即可得到事件![]() 的概率.
的概率.
(2)由题意得,得到随机变量![]() 的所有可能取值,求得随机变量取每个值的概率,即可得到随机变量的分布列,并计算其数学期望.
的所有可能取值,求得随机变量取每个值的概率,即可得到随机变量的分布列,并计算其数学期望.
试题解析:
(1)由已知得![]() .所以事件
.所以事件![]() 发生的概率为
发生的概率为![]() .
.
(2)随机变量![]() 的所有可能取值为0,1,2
的所有可能取值为0,1,2
计算![]() ,
,
![]() ,
,
![]() ;
;
所以随机变量![]() 的分布列为:
的分布列为:

随机变量![]() 的数学期望为
的数学期望为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果如下表所示:
休假次数
0
1
2
3
人数
5
10
20
15
根据表中信息解答以下问题:
(1)从该单位任选两名职工,求这两人休年假次数之和为4的概率;
(2)从该单位任选两名职工,用
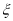 表示这两人休年假次数之差的绝对值,求随机变量
表示这两人休年假次数之差的绝对值,求随机变量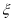 的分布列及数学期望
的分布列及数学期望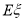 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】用秦九韶算法求多项式f(x)=x6-5x5+6x4+x2+0.3x+2当x=-2时的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校课题组为了研究学生的数学成绩与学生细心程度的关系,在本校随机调查了100名学生进行研究.研究结果表明:在数学成绩及格的60名学生中有45人比较细心,另外15人比较粗心;在数学成绩不及格的40名学生中有10人比较细心,另外30人比较粗心.
(1)试根据上述数据完成
 列联表;
列联表;数学成绩及格
数学成绩不及格
合计
比较细心
45
比较粗心
合计
60
100
(2)能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系?
参考数据:独立检验随机变量
 的临界值参考表:
的临界值参考表: 
0.15
0.10
0.05
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
 ,其中
,其中
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
设函数
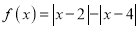 .
.(1)求解不等式
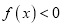 的解集;
的解集;(2)若函数
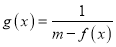 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
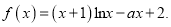
(1)当
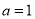 时,求函数
时,求函数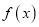 在
在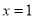 处的切线方程;
处的切线方程;(2)若函数
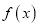 在定义域上具有单调性,求实数
在定义域上具有单调性,求实数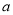 的取值范围;
的取值范围;(3)求证:
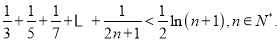
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面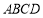 为菱形,
为菱形, ,
,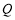 为
为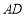 的中点.
的中点.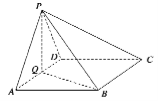
(1)若
 ,求证:
,求证: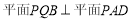 ;
;(2)若
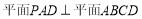 ,且
,且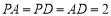 ,点
,点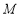 在线段
在线段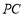 上,试确定点
上,试确定点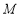 的位置,使二面角
的位置,使二面角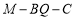 大小为
大小为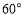 ,并求出
,并求出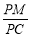 的值.
的值.
相关试题

