【题目】已知函数![]()
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在定义域上具有单调性,求实数
在定义域上具有单调性,求实数![]() 的取值范围;
的取值范围;
(3)求证: ![]()
参考答案:
【答案】(1)![]() (2)a≤2.(3)详见解析
(2)a≤2.(3)详见解析
【解析】试题分析:(1)由导数几何意义得切线斜率等于该点处导数值,再利用点斜式求切线方程,(2)先按单调递增与单调递减分类讨论,再将函数单调性转化为函数导数值恒非负或非正,利用变量分离转化为求对应函数最值,进而确定实数![]() 的取值范围;(3)利用导数证明数列求和不等式,一般方法为先构造目标函数(利用前面小题的结论),再代入数列,利用裂项相消法放缩求和,进而得证不等式.
的取值范围;(3)利用导数证明数列求和不等式,一般方法为先构造目标函数(利用前面小题的结论),再代入数列,利用裂项相消法放缩求和,进而得证不等式.
试题解析:(1)当a=1时,f(x)=(x+1)lnx﹣x+2,(x>0),
f′(x)=lnx+![]() ,f′(1)=1,f(1)=1,
,f′(1)=1,f(1)=1,
所以求在x=1处的切线方程为:y=x
(2)f′(x)=lnx+![]() +1﹣a,(x>0).
+1﹣a,(x>0).
(i)函数f(x)在定义域上单调递减时,
即a≥lnx+![]() 时,令g(x)=lnx+
时,令g(x)=lnx+![]() ,
,
当x>ea时,g′(x)>0,不成立;
(ii)函数f(x)在定义域上单调递增时,a≤lnx+![]() ;
;
令g(x)=lnx+![]() ,
,
则g′(x)=![]() ,x>0;
,x>0;
则函数g(x)在(0,1)上单调递减,在(1,+∞)上单调递增;
所以g(x)≥2,故a≤2.
(3)由(ii)得当a=2时f(x)在(1,+∞)上单调递增,
由f(x)>f(1),x>1得(x+1)lnx﹣2x+2>0,
即lnx>![]() 在(1,+∞)上总成立,
在(1,+∞)上总成立,
令x=![]() 得ln
得ln![]() >
>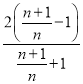 ,
,
化简得:ln(n+1)﹣lnn>![]() ,
,
所以ln2﹣ln1>![]() ,
,
ln3﹣ln2>![]() ,…,
,…,
ln(n+1)﹣lnn>![]() ,
,
累加得ln(n+1)﹣ln1>![]() ,
,
即![]() 命题得证.
命题得证.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校课题组为了研究学生的数学成绩与学生细心程度的关系,在本校随机调查了100名学生进行研究.研究结果表明:在数学成绩及格的60名学生中有45人比较细心,另外15人比较粗心;在数学成绩不及格的40名学生中有10人比较细心,另外30人比较粗心.
(1)试根据上述数据完成
 列联表;
列联表;数学成绩及格
数学成绩不及格
合计
比较细心
45
比较粗心
合计
60
100
(2)能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系?
参考数据:独立检验随机变量
 的临界值参考表:
的临界值参考表: 
0.15
0.10
0.05
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
 ,其中
,其中
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小组共10人,利用假期参加义工活动,已知参加义工活动1次的有2人,2次的有4人,3次的有4人.现从这10人中随机选出2人作为该组代表参加座谈会.
(1)设
 为事件“选出的2人参加义工活动次数之和为4”,求事件
为事件“选出的2人参加义工活动次数之和为4”,求事件 发生的概率;
发生的概率;(2)设
 为选出的2人参加义工活动次数之差的绝对值,求随机变量
为选出的2人参加义工活动次数之差的绝对值,求随机变量 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
设函数
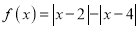 .
.(1)求解不等式
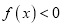 的解集;
的解集;(2)若函数
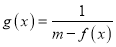 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面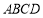 为菱形,
为菱形, ,
,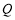 为
为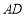 的中点.
的中点.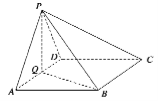
(1)若
 ,求证:
,求证: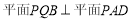 ;
;(2)若
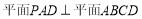 ,且
,且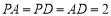 ,点
,点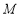 在线段
在线段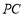 上,试确定点
上,试确定点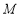 的位置,使二面角
的位置,使二面角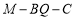 大小为
大小为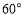 ,并求出
,并求出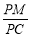 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.2017年1月某日某省x个监测点数据统计如下:
空气污染指数
(单位:μg/m3)




监测点个数
15
40
y
10
(1)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(2)若A市共有5个监测点,其中有3个监测点为轻度污染,2个监测点为良.从中任意选取2个监测点,事件A“其中至少有一个为良”发生的概率是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
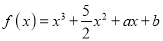 ,
, 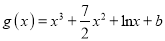 ,(
,( 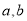 为常数)
为常数)(1)若
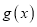 在
在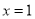 处的切线方程为
处的切线方程为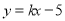 (
(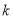 为常数),求
为常数),求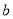 的值;
的值;(2)设函数
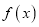 的导函数为
的导函数为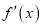 ,若存在唯一的实数
,若存在唯一的实数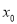 ,使得
,使得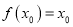 与
与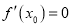 同时成立,求实数
同时成立,求实数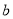 的取值范围;
的取值范围;(3)令
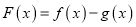 ,若函数
,若函数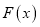 存在极值,且所有极值之和大于
存在极值,且所有极值之和大于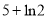 ,求
,求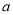 的取值范围.
的取值范围.
相关试题

