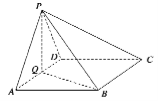
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)若![]() ,求证:
,求证:![]() ;
;
(2)若![]() ,且
,且![]() ,点
,点![]() 在线段
在线段![]() 上,试确定点
上,试确定点![]() 的位置,使二面角
的位置,使二面角![]() 大小为
大小为![]() ,并求出
,并求出![]() 的值.
的值.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)由![]() ,
,![]() 为
为![]() 的中点,得
的中点,得![]() ,又由底面
,又由底面![]() 为菱形,根据菱形的性质,证得
为菱形,根据菱形的性质,证得![]() ,进而证得
,进而证得![]() ,即可证明
,即可证明![]() ;(2)以
;(2)以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 、
、![]() 、
、![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,得平面
轴建立空间直角坐标系,得平面![]() 和平面
和平面![]() 的一个法向量,根据二面角
的一个法向量,根据二面角![]() 大小为
大小为![]() ,利用向量的运算,即可求解求出
,利用向量的运算,即可求解求出![]() 的值.
的值.
试题解析:⑴∵![]() ,
,![]() 为
为![]() 的中点,∴
的中点,∴![]() ,又∵底面
,又∵底面![]() 为菱形,
为菱形,![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]() ,又∵
,又∵![]() ,∴
,∴![]() ;
;
⑵∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴以
,∴以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 、
、![]() 、
、![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系如图.
轴建立空间直角坐标系如图.
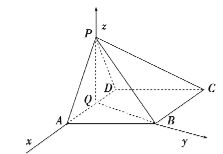
则![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,
所以![]() ,平面
,平面![]() 的一个法向量是
的一个法向量是![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以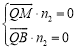 ,∴
,∴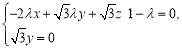 ∴
∴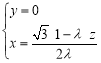 .
.
取![]() ,
,
由二面角![]() 大小为
大小为![]() ,可得:
,可得:![]() ,解得
,解得![]() ,此时
,此时![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小组共10人,利用假期参加义工活动,已知参加义工活动1次的有2人,2次的有4人,3次的有4人.现从这10人中随机选出2人作为该组代表参加座谈会.
(1)设
 为事件“选出的2人参加义工活动次数之和为4”,求事件
为事件“选出的2人参加义工活动次数之和为4”,求事件 发生的概率;
发生的概率;(2)设
 为选出的2人参加义工活动次数之差的绝对值,求随机变量
为选出的2人参加义工活动次数之差的绝对值,求随机变量 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
设函数
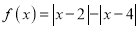 .
.(1)求解不等式
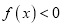 的解集;
的解集;(2)若函数
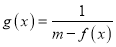 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
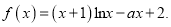
(1)当
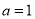 时,求函数
时,求函数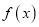 在
在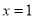 处的切线方程;
处的切线方程;(2)若函数
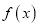 在定义域上具有单调性,求实数
在定义域上具有单调性,求实数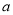 的取值范围;
的取值范围;(3)求证:
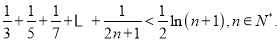
-
科目: 来源: 题型:
查看答案和解析>>【题目】空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.2017年1月某日某省x个监测点数据统计如下:
空气污染指数
(单位:μg/m3)




监测点个数
15
40
y
10
(1)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(2)若A市共有5个监测点,其中有3个监测点为轻度污染,2个监测点为良.从中任意选取2个监测点,事件A“其中至少有一个为良”发生的概率是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
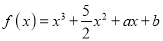 ,
, 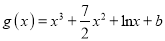 ,(
,( 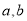 为常数)
为常数)(1)若
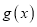 在
在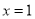 处的切线方程为
处的切线方程为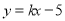 (
(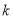 为常数),求
为常数),求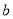 的值;
的值;(2)设函数
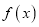 的导函数为
的导函数为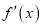 ,若存在唯一的实数
,若存在唯一的实数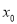 ,使得
,使得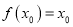 与
与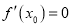 同时成立,求实数
同时成立,求实数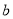 的取值范围;
的取值范围;(3)令
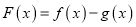 ,若函数
,若函数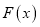 存在极值,且所有极值之和大于
存在极值,且所有极值之和大于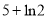 ,求
,求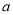 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(A)在直角坐标系
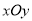 中,以坐标原点为极点,
中,以坐标原点为极点, 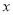 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线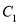 的参数方程为
的参数方程为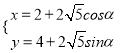 (
(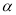 为参数),
为参数), 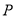 是曲线
是曲线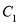 上的动点,
上的动点, 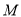 为线段
为线段 的中点,设点
的中点,设点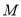 的轨迹为曲线
的轨迹为曲线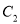 .
.(1)求
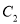 的坐标方程;
的坐标方程;(2)若射线
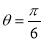 与曲线
与曲线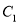 异于极点的交点为
异于极点的交点为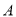 ,与曲线
,与曲线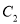 异于极点的交点为
异于极点的交点为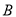 ,求
,求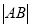 .
.
相关试题

