搜索
【题目】解关于
的不等式
．
参考答案：
【答案】见解析
【解析】分析：先讨论二次项系数为零的情况，再讨论开口向上与向下的情况，注意比较两根大小关系.
详解：当m=0时，不等式化为x+2＜0，解得解集为（﹣∞，﹣2）；
当m＞0时，不等式等价于（x﹣
）（x+2）＞0，
解得不等式的解集为（﹣∞，﹣2）∪（，+∞）；
当m＜0时，不等式等价于（x﹣）（x+2）＜0，
若﹣
＜m＜0，则＜﹣2，解得不等式的解集为（
，﹣2）；
若m=﹣
，则=﹣2，不等式化为（x+2）2＜0，此时不等式的解集为；
若m＜﹣，则＞﹣2，解得不等式的解集为（﹣2，）．
综上，m=0时，不等式的解集为（﹣∞，﹣2）；
m＞0时，不等式的解集为（﹣∞，﹣2）∪（，+∞）；
﹣＜m＜0时，不等式的解集为（，﹣2）；
m=﹣时，不等式的解集为；
m＜﹣时，不等式的解集为（﹣2，
）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】用
这六个数字.（1）能组成多少个无重复数字的四位偶数？
（2）能组成多少个无重复数字且为
的倍数的五位数？（3）能组成多少个无重复数字且比
大的四位数？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知复数z＝
＋(a2－5a－6)i(a∈R)．试求实数a分别为什么值时，z分别为(1)实数？(2)虚数？(3)纯虚数？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
.（1）求
的值；（2）若函数
在区间
是单调递增函数，求实数
的取值范围；（3）若关于
的方程
在区间
内有两个实数根
，记
，求实数
的取值范围 . -
科目： 来源： 题型：
查看答案和解析>>【题目】已知A(2,0)，B(0,2)，
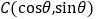，O为坐标原点．（1）
，求sin 2θ的值；（2）若
，且θ∈(－π,0)，求
与
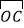的夹角． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，O为坐标原点，M为平面上任一点，A，B，C三点满足
．（1）求
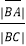的值；（2）已知A(1,sinx)、B(1+sinx,sinx)，M(1+
sinx,sinx)，x∈(0,π)，且函数
的最小值为
，求实数m的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】设复数z＝2m＋(4－m2)i，当实数m取何值时，复数z对应的点：
(1)位于虚轴上？
(2)位于一、三象限？
(3)位于以原点为圆心，以4为半径的圆上？
相关试题
