【题目】已知函数![]() .
.
(1)求![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 是单调递增函数,求实数
是单调递增函数,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 内有两个实数根
内有两个实数根![]() ,记
,记![]() ,求实数
,求实数![]() 的取值范围 .
的取值范围 .
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
分析:(1)先根据二倍角公式以及配角公式化为基本三角函数,再代入求![]() 的值;(2)根据正弦函数性质确定单调性递增区间,再根据区间之间包含关系列不等式,解得实数
的值;(2)根据正弦函数性质确定单调性递增区间,再根据区间之间包含关系列不等式,解得实数![]() 的取值范围;(3)先根据正弦函数图像确定a的取值范围,再根据对称性得
的取值范围;(3)先根据正弦函数图像确定a的取值范围,再根据对称性得![]() ,最后代入求实数
,最后代入求实数![]() 的取值范围.
的取值范围.
详解:
(Ⅰ)∵![]()
![]()
![]()
∴![]()
(Ⅱ)由![]() ,
,![]()
得![]() ,
,![]()
∴![]() 在区间
在区间![]() 上是增函数
上是增函数
∴当![]() 时,
时,![]() 在区间
在区间![]() 上是增函数
上是增函数
若函数![]() 在区间
在区间![]() 上是单调递增函数,则
上是单调递增函数,则![]()
∴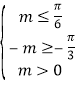 ,解得
,解得![]()
(Ⅲ)方程![]() 在区间
在区间![]() 内有两实数根
内有两实数根![]() 等价于直线
等价于直线![]() 与曲线
与曲线![]()
![]() 有两个交点.
有两个交点.
∵当![]() 时,由(Ⅱ)知
时,由(Ⅱ)知![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,且
上是减函数,且![]() ,
,![]() ,
,![]() ,
,
∴![]()
即实数![]() 的取值范围是
的取值范围是![]()
∵函数![]() 的图像关于
的图像关于![]() 对称
对称
∴![]() ,∴
,∴![]()
∴实数![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租时间不超过两小时免费,超过两个小时的部分每小时收费2元(不足1小时的部分按 1小时计算).有甲、乙两人独立来该租车点租车骑游(各租一车一次).设甲、乙不超过两小时还车的概率分别为
 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为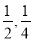 ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.(1)求甲、乙两人所付租车费用相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量
 ,求
,求 的分布列.
的分布列. -
科目: 来源: 题型:
查看答案和解析>>【题目】用
 这六个数字.
这六个数字.(1)能组成多少个无重复数字的四位偶数?
(2)能组成多少个无重复数字且为
 的倍数的五位数?
的倍数的五位数?(3)能组成多少个无重复数字且比
 大的四位数?
大的四位数? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知复数z=
 +(a2-5a-6)i(a∈R).试求实数a分别为什么值时,z分别为(1)实数?(2)虚数?(3)纯虚数?
+(a2-5a-6)i(a∈R).试求实数a分别为什么值时,z分别为(1)实数?(2)虚数?(3)纯虚数? -
科目: 来源: 题型:
查看答案和解析>>【题目】解关于
 的不等式
的不等式 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(2,0),B(0,2),
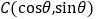 ,O为坐标原点.
,O为坐标原点.(1)
 ,求sin 2θ的值;
,求sin 2θ的值;(2)若
 ,且θ∈(-π,0),求
,且θ∈(-π,0),求 与
与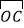 的夹角.
的夹角. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,M为平面上任一点,A,B,C三点满足
 .
.(1)求
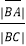 的值;
的值;(2)已知A(1,sinx)、B(1+sinx,sinx),M(1+
 sinx,sinx),x∈(0,π),且函数
sinx,sinx),x∈(0,π),且函数 的最小值为
的最小值为 ,求实数m的值.
,求实数m的值.
相关试题

