【题目】已知A(2,0),B(0,2),![]() ,O为坐标原点.
,O为坐标原点.
(1)![]() ,求sin 2θ的值;
,求sin 2θ的值;
(2)若![]() ,且θ∈(-π,0),求
,且θ∈(-π,0),求![]() 与
与![]() 的夹角.
的夹角.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
分析:(1) 先根据向量数量积得sin θ+cos θ值,再平方得结果,(2)先根据向量的模得cos θ,即得C点坐标,再根据向量夹角公式求结果.
详解:(1)∵![]() =(cos θ,sinθ)-(2,0)=(cos θ-2,sin θ),
=(cos θ,sinθ)-(2,0)=(cos θ-2,sin θ),
![]() =(cos θ,sin θ)-(0,2)=(cos θ,sin θ-2),
=(cos θ,sin θ)-(0,2)=(cos θ,sin θ-2),
![]() =cos θ(cos θ-2)+sin θ(sin θ-2)=cos2θ-2cos θ+sin2θ-2sin θ=1-2(sin θ+cos θ)=-
=cos θ(cos θ-2)+sin θ(sin θ-2)=cos2θ-2cos θ+sin2θ-2sin θ=1-2(sin θ+cos θ)=-
∴sin θ+cos θ=,
∴1+2sin θcos θ=![]() ,
,
∴sin 2θ=![]() -1=-.
-1=-.
(2)∵![]() =(2,0),
=(2,0),![]() =(cos θ,sin θ),
=(cos θ,sin θ),
∴![]() +
+![]() =(2+cos θ,sin θ),
=(2+cos θ,sin θ),
∵|![]() +
+![]() |=
|=![]() ,所以4+4cos θ+cos2θ+sin2θ=7,
,所以4+4cos θ+cos2θ+sin2θ=7,
∴4cos θ=2,即cos θ=.
∵-π<θ<0,∴θ=-![]() ,
,
又∵![]() =(0,2),
=(0,2),![]() =
=![]() ,
,
∴cos〈![]() ,
,![]() 〉=
〉=![]() ,∴〈
,∴〈![]() ,
,![]() 〉=
〉=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知复数z=
 +(a2-5a-6)i(a∈R).试求实数a分别为什么值时,z分别为(1)实数?(2)虚数?(3)纯虚数?
+(a2-5a-6)i(a∈R).试求实数a分别为什么值时,z分别为(1)实数?(2)虚数?(3)纯虚数? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求
 的值;
的值;(2)若函数
 在区间
在区间 是单调递增函数,求实数
是单调递增函数,求实数 的取值范围;
的取值范围;(3)若关于
 的方程
的方程 在区间
在区间 内有两个实数根
内有两个实数根 ,记
,记 ,求实数
,求实数 的取值范围 .
的取值范围 . -
科目: 来源: 题型:
查看答案和解析>>【题目】解关于
 的不等式
的不等式 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,M为平面上任一点,A,B,C三点满足
 .
.(1)求
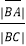 的值;
的值;(2)已知A(1,sinx)、B(1+sinx,sinx),M(1+
 sinx,sinx),x∈(0,π),且函数
sinx,sinx),x∈(0,π),且函数 的最小值为
的最小值为 ,求实数m的值.
,求实数m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设复数z=2m+(4-m2)i,当实数m取何值时,复数z对应的点:
(1)位于虚轴上?
(2)位于一、三象限?
(3)位于以原点为圆心,以4为半径的圆上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一名学生骑自行车上学,从他家到学校的途中有
 个交通岗,假设他在各个交通岗遇到红灯的事件是相互独立的,并且概率都是
个交通岗,假设他在各个交通岗遇到红灯的事件是相互独立的,并且概率都是 .求:
.求:(
 )这名学生在途中遇到
)这名学生在途中遇到 次红灯次数的概率.
次红灯次数的概率.(
 )这名学生在首次停车前经过了
)这名学生在首次停车前经过了 个路口的概率.
个路口的概率.(
 )这名学生至少遇到一次红灯的概率.
)这名学生至少遇到一次红灯的概率.
相关试题

