【题目】用![]() 这六个数字.
这六个数字.
(1)能组成多少个无重复数字的四位偶数?
(2)能组成多少个无重复数字且为![]() 的倍数的五位数?
的倍数的五位数?
(3)能组成多少个无重复数字且比![]() 大的四位数?
大的四位数?
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1)符合要求的四位可分为三类:第一类:![]() 在个位时有
在个位时有![]() 个;
个;
第二类:![]() 在个位时,首位从
在个位时,首位从![]() 中选定
中选定![]() 个(有
个(有![]() 种),十位和百位从余下的数字中选(有
种),十位和百位从余下的数字中选(有![]() 种),于是有
种),于是有![]() 个;
个;
第三类:![]() 在个位时,与第二类同理,也有
在个位时,与第二类同理,也有![]() 个,由分类加法计算原理知,共有四位偶数
个,由分类加法计算原理知,共有四位偶数![]() 个.
个.
(2)符合要求的五位数可分为两类:个位数上的数字是![]() 的五位数有
的五位数有![]() 个,个位数上的数字是
个,个位数上的数字是![]() 的五位数有
的五位数有![]() 个,故满足条件的五位数的个数共有
个,故满足条件的五位数的个数共有![]() 个.
个.
(3)比![]() 大的四位偶数可分为三类:
大的四位偶数可分为三类:
第一类:形如![]() 共有
共有![]() 个;
个;
第二类:形如![]() , 共有
, 共有![]() 个;
个;
第三类:形如![]() ,共有
,共有![]() 个.
个.
由分类加法计数原理知,无重复数字且比![]() 大的四位数共有
大的四位数共有![]() 个.
个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在女子十米跳台比赛中,已知甲、乙两名选手发挥正常的概率分别为0.9,0.85,求:
(1)甲、乙两名选手发挥均正常的概率;
(2)甲、乙两名选手至多有一名发挥正常的概率;
(3)甲、乙两名选手均出现失误的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 (e为自然对数的底).若函数g(x)=f(x)﹣kx恰好有两个零点,则实数k的取值范围是( )
(e为自然对数的底).若函数g(x)=f(x)﹣kx恰好有两个零点,则实数k的取值范围是( )
A.(1,e)
B.(e,10]
C.(1,10]
D.(10,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租时间不超过两小时免费,超过两个小时的部分每小时收费2元(不足1小时的部分按 1小时计算).有甲、乙两人独立来该租车点租车骑游(各租一车一次).设甲、乙不超过两小时还车的概率分别为
 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为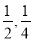 ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.(1)求甲、乙两人所付租车费用相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量
 ,求
,求 的分布列.
的分布列. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知复数z=
 +(a2-5a-6)i(a∈R).试求实数a分别为什么值时,z分别为(1)实数?(2)虚数?(3)纯虚数?
+(a2-5a-6)i(a∈R).试求实数a分别为什么值时,z分别为(1)实数?(2)虚数?(3)纯虚数? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求
 的值;
的值;(2)若函数
 在区间
在区间 是单调递增函数,求实数
是单调递增函数,求实数 的取值范围;
的取值范围;(3)若关于
 的方程
的方程 在区间
在区间 内有两个实数根
内有两个实数根 ,记
,记 ,求实数
,求实数 的取值范围 .
的取值范围 . -
科目: 来源: 题型:
查看答案和解析>>【题目】解关于
 的不等式
的不等式 .
.
相关试题

