【题目】![]() 的内角
的内角![]() 的对边分别为
的对边分别为![]() ,已知
,已知![]() .
.
(1)求![]() ;
;
(2)若![]() ,求
,求![]() 的面积.
的面积.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由正弦定理得 sinA=sinBcosC+![]() sinCsinB,从而cosBsinC=
sinCsinB,从而cosBsinC=![]() sinCsinB,进而tanB=
sinCsinB,进而tanB=![]() ,由此能求出B.(2)利用余弦定理得a,由此能求出△ABC的面积.
,由此能求出B.(2)利用余弦定理得a,由此能求出△ABC的面积.
(1)由a=bcosC+![]() csinB及正弦定理,可得:sinA=sinBcosC+
csinB及正弦定理,可得:sinA=sinBcosC+![]() sinCsinB,①
sinCsinB,①
又sinA=sin(π﹣B﹣C)=sin(B+C)=sinBcosC+cosBsinC②,由①②得![]() sinCsinB=cosBsinC,又三角形中,sinC≠0,所以
sinCsinB=cosBsinC,又三角形中,sinC≠0,所以![]() sinB=cosB,又B∈(0,π),所以B=
sinB=cosB,又B∈(0,π),所以B=![]() .
.
(2)△ABC的面积为S=![]() =
=![]() .由余弦定理,b2=a2+c2﹣2accosB,得4=a2+c2﹣
.由余弦定理,b2=a2+c2﹣2accosB,得4=a2+c2﹣![]() ,又
,又![]() ,得c2=4c=2,
,得c2=4c=2,![]() ,所以△ABC的面积为
,所以△ABC的面积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,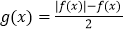
(1)写出函数
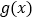 的解析式;
的解析式;(2)若直线
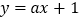 与曲线
与曲线 有三个不同的交点,求
有三个不同的交点,求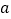 的取值范围;
的取值范围;(3)若直线
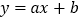 与曲线
与曲线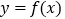 在
在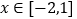 内有交点,求
内有交点,求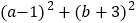 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
 中,
中, 底面
底面 ,
, ,
, ,
, ,
, ,点
,点 在
在 上
上
(1)求证:
 平面
平面 ;
;(2)当
 平面
平面 时,求
时,求 的值
的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】 由经验得知,在某商场付款处排队等候付款的人数及概率如下表
排队人数
0
1
2
3
4
5人以上
概率
0.1
0.16
0.3
0.3
0.1
0.04
(1)至多有2人排队的概率是多少?
(2)至少有2人排队的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是东西方向的公路北侧的边缘线,某公司准备在
是东西方向的公路北侧的边缘线,某公司准备在 上的一点
上的一点 的正北方向的
的正北方向的 处建设一仓库,设
处建设一仓库,设 ,并在公路北侧建造边长为
,并在公路北侧建造边长为 的正方形无顶中转站
的正方形无顶中转站 (其中
(其中 在
在 上),现从仓库
上),现从仓库 向
向 和中转站分别修两条道路
和中转站分别修两条道路 ,已知
,已知 ,且
,且 .
.
(1)求
 关于
关于 的函数解析式,并求出定义域;
的函数解析式,并求出定义域;(2)如果中转站四堵围墙造价为10万元
 ,两条道路造价为30万元
,两条道路造价为30万元 ,问:
,问: 取何值时,该公司建设中转站围墙和两条道路总造价
取何值时,该公司建设中转站围墙和两条道路总造价 最低.
最低. -
科目: 来源: 题型:
查看答案和解析>>【题目】“共享单车”的出现,为我们提供了一种新型的交通方式.某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:

(Ⅰ)根据茎叶图,比较两城市满意度评分的平均值的大小及方差的大小(不要求计算出具体值,给出结论即可);
(Ⅱ)若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成此2×2列联表,并据此样本分析是否有95%的把握认为城市拥堵与认可共享单车有关;A
B
合计
认可
不认可
合计
(Ⅲ)若从此样本中的A城市和B城市各抽取1人,则在此2人中恰有一人认可的条件下,此人来自B城市的概率是多少?
附:参考数据:
(参考公式: )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱ABC﹣A1B1C1中,侧面AA1B1B⊥底面ABC,△ABC和△ABB1都是边长为2的正三角形.

(Ⅰ)过B1作出三棱柱的截面,使截面垂直于AB,并证明;
(Ⅱ)求AC1与平面BCC1B1所成角的正弦值.
相关试题

