【题目】在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上
上

(1)求证:![]() 平面
平面![]() ;
;
(2)当![]() 平面
平面![]() 时,求
时,求![]() 的值
的值
参考答案:
【答案】(1)证明见解析;(2)2.
【解析】
(1)作出辅助线,然后利用线面垂直的判定定理即可证得题中的结论;
(2)作出辅助线,首先由线面平行的判定定理将原问题进行转化,然后利用平行线分线段成比例定理即可求得![]() 的值.
的值.
(1)过A作AF⊥DC于F,则CF=DF=AF,所以∠DAC=90°,即AC⊥DA,
又PA⊥底面ABCD,AC面ABCD,所以AC⊥PA,
因为PA、AD面PAD,且PA∩AD=A,所以AC⊥平面PAD.

(2)连接BD交AC于点O,连接EO,
因为PD∥平面AEC,PD面PBD,面PBD∩面AEC=EO,所以PD∥EO
则PE:EB=DO:OB,而DO:OB=DC:AB=2,所以PE:EB=2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
 的右顶点为A,上顶点为B.已知椭圆的离心率为
的右顶点为A,上顶点为B.已知椭圆的离心率为 ,
, .
.(1)求椭圆的方程;
(2)设直线
 与椭圆交于
与椭圆交于 ,
, 两点,
两点, 与直线
与直线 交于点M,且点P,M均在第四象限.若
交于点M,且点P,M均在第四象限.若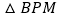 的面积是
的面积是 面积的2倍,求
面积的2倍,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】
 是定义在R上的函数,对
是定义在R上的函数,对 ∈R都有
∈R都有 ,且当
,且当 >0时,
>0时, <0,且
<0,且 =1.
=1.(1)求
 的值;
的值;(2)求证:
 为奇函数;
为奇函数;(3)求
 在[-2,4]上的最值.
在[-2,4]上的最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,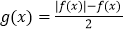
(1)写出函数
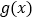 的解析式;
的解析式;(2)若直线
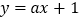 与曲线
与曲线 有三个不同的交点,求
有三个不同的交点,求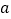 的取值范围;
的取值范围;(3)若直线
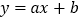 与曲线
与曲线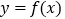 在
在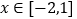 内有交点,求
内有交点,求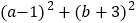 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】 由经验得知,在某商场付款处排队等候付款的人数及概率如下表
排队人数
0
1
2
3
4
5人以上
概率
0.1
0.16
0.3
0.3
0.1
0.04
(1)至多有2人排队的概率是多少?
(2)至少有2人排队的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 的内角
的内角 的对边分别为
的对边分别为 ,已知
,已知 .
.(1)求
 ;
;(2)若
 ,求
,求 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是东西方向的公路北侧的边缘线,某公司准备在
是东西方向的公路北侧的边缘线,某公司准备在 上的一点
上的一点 的正北方向的
的正北方向的 处建设一仓库,设
处建设一仓库,设 ,并在公路北侧建造边长为
,并在公路北侧建造边长为 的正方形无顶中转站
的正方形无顶中转站 (其中
(其中 在
在 上),现从仓库
上),现从仓库 向
向 和中转站分别修两条道路
和中转站分别修两条道路 ,已知
,已知 ,且
,且 .
.
(1)求
 关于
关于 的函数解析式,并求出定义域;
的函数解析式,并求出定义域;(2)如果中转站四堵围墙造价为10万元
 ,两条道路造价为30万元
,两条道路造价为30万元 ,问:
,问: 取何值时,该公司建设中转站围墙和两条道路总造价
取何值时,该公司建设中转站围墙和两条道路总造价 最低.
最低.
相关试题

