【题目】从某企业生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.

(Ⅰ)求这些产品质量指标值落在区间![]() 内的频率;
内的频率;
(Ⅱ)用分层抽样的方法在区间![]() 内抽取一个容量为6的样本,将该样本看成一个总体,从中任意
内抽取一个容量为6的样本,将该样本看成一个总体,从中任意
抽取2件产品,求这2件产品都在区间![]() 内的概率.
内的概率.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)利用频率分布直方图中所有频率之和等于![]() 可得这些产品质量指标值落在区间
可得这些产品质量指标值落在区间![]() 内的频率;(Ⅱ)先算出落在区间
内的频率;(Ⅱ)先算出落在区间![]() ,
,![]() ,
,![]() 内的产品件数,再列举出从
内的产品件数,再列举出从![]() 件产品中任意抽取
件产品中任意抽取![]() 件产品的基本事件和这
件产品的基本事件和这![]() 件产品都在区间
件产品都在区间![]() 内的基本事件,进而利用古典概型公式可得这
内的基本事件,进而利用古典概型公式可得这![]() 件产品都在区间
件产品都在区间![]() 内的概率.
内的概率.
试题解析:(Ⅰ)设区间![]() 内的频率为
内的频率为![]() ,
,
则区间![]() ,
,![]() 内的频率分别为
内的频率分别为![]() 和
和![]() .
.
依题意得![]() ,
,
解得![]() .
.
所以区间![]() 内的频率为
内的频率为![]() .
.
(Ⅱ)由(Ⅰ)得,区间![]() ,
,![]() ,
,![]() 内的频率依次为
内的频率依次为![]() ,
,![]() ,
,![]() .
.
用分层抽样的方法在区间![]() 内抽取一个容量为6的样本,
内抽取一个容量为6的样本,
则在区间![]() 内应抽取
内应抽取![]() 件,记为
件,记为![]() ,
,![]() ,
,![]() .
.
在区间![]() 内应抽取
内应抽取![]() 件,记为
件,记为![]() ,
,![]() .
.
在区间![]() 内应抽取
内应抽取![]() 件,记为
件,记为![]() .
.
设“从样本中任意抽取2件产品,这2件产品都在区间![]() 内”为事件M,
内”为事件M,
则所有的基本事件有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共15种.
,共15种.
事件M包含的基本事件有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共10种.
,共10种.
所以这2件产品都在区间![]() 内的概率为
内的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
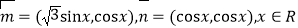 ,设
,设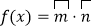 .
.(1)求函数
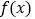 的解析式及单调递增区间;
的解析式及单调递增区间;(2)在
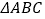 中,
中,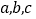 分别为内角
分别为内角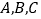 的对边,且
的对边,且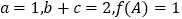 ,求
,求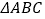 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知Sn是正项数列{an}的前n项和,且Sn=
 an2+
an2+  an﹣
an﹣ 
(1)求数列{an}的通项公式;
(2)若an=2nbn , 求数列{bn}的前n项和. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系
 中,圆
中,圆 与
与 轴负半轴交于点
轴负半轴交于点 ,过点
,过点 的直线
的直线 ,
, 分别与圆
分别与圆 交于
交于 ,
, 两点.
两点.
(Ⅰ)若
 ,
, ,求
,求 的面积;
的面积;(Ⅱ)若直线
 过点
过点 ,证明:
,证明: 为定值,并求此定值.
为定值,并求此定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某几何体的三视图如下图,则该几何体的体积为( )
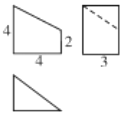
A. 18 B. 20 C. 24 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , 若4Sn=(2n﹣1)an+1+1,且a1=1.
(1)求数列{an}的通项公式;
(2)设cn=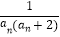 ,数列{cn}的前n项和为Tn .
,数列{cn}的前n项和为Tn .
①求Tn;
②对于任意的n∈N*及x∈R,不等式kx2﹣6kx+k+7+3Tn>0恒成立,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】 用总长14.8米的钢条制作一个长方体容器的框架,如果所制容器底面一边的长比另一边的长多0.5米,那么高为多少时容器的容积最大?最大容积是多少?
相关试题

