【题目】已知向量![]() ,设
,设![]() .
.
(1)求函数![]() 的解析式及单调递增区间;
的解析式及单调递增区间;
(2)在![]() 中,
中,![]() 分别为内角
分别为内角![]() 的对边,且
的对边,且![]() ,求
,求![]() 的面积.
的面积.
参考答案:
【答案】(1)[-![]() ]
]![]() ;(2)面积为
;(2)面积为 ![]()
【解析】试题分析:
(I)根据向量数量积的坐标公式得出f(x),利用二倍角公式,两角和的正弦函数公式化简,根据正弦函数的单调性得出f(x)的单调区间;
(II)根据f(A)=1和A的范围解出A,利用余弦定理得出bc,代入面积公式S=![]() bcsinA即可.
bcsinA即可.
解:
(I)f(x)=![]() sinxcosx+cos2x=
sinxcosx+cos2x=![]() sin2x+
sin2x+![]() cos2x+
cos2x+![]() =
=![]() .
.
![]() ,
,![]() .得[-
.得[-![]() ]
]![]() .
.
所以函数的单调递增区间为[-![]() ]
]![]() .
.
(II)∵f(A)=sin(2A+![]() )+
)+![]() =1,∴sin(2A+
=1,∴sin(2A+![]() )=
)=![]() .
.
∵0<A<π,∴![]() <2A+
<2A+![]() <
<![]() ,∴2A+
,∴2A+![]() =
=![]() ,即A=
,即A=![]() .
.
由余弦定理得:a2=b2+c2﹣2bccosA=(b+c)2﹣2bc﹣2bccosA,∴1=4﹣3bc,∴bc=1.
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABC中,内角A,B,C的对边分别为a,b,c,已知
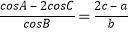
(1)求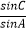 的值;
的值;
(2)若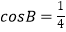 ,b=2,求△ABC的面积S.
,b=2,求△ABC的面积S. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
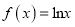 ,
, 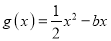 (
(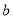 为常数).
为常数).(1)函数
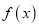 的图象在点
的图象在点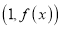 处的切线与函数
处的切线与函数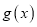 的图象相切,求实数
的图象相切,求实数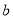 的值;
的值;(2)若函数
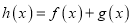 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数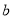 的取值范围;
的取值范围;(3)若
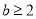 ,
, 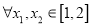 ,且
,且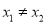 ,都有
,都有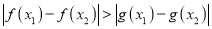 成立,求实数
成立,求实数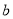 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
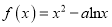 (
(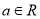 ),
),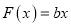 (
(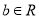 ).
).(1)讨论
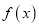 的单调性;
的单调性;(2)设
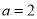 ,
, 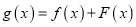 ,若
,若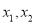 (
(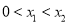 )是
)是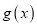 的两个零点,且
的两个零点,且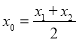 ,
,试问曲线
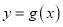 在点
在点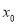 处的切线能否与
处的切线能否与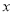 轴平行?请说明理由.
轴平行?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知Sn是正项数列{an}的前n项和,且Sn=
 an2+
an2+  an﹣
an﹣ 
(1)求数列{an}的通项公式;
(2)若an=2nbn , 求数列{bn}的前n项和. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系
 中,圆
中,圆 与
与 轴负半轴交于点
轴负半轴交于点 ,过点
,过点 的直线
的直线 ,
, 分别与圆
分别与圆 交于
交于 ,
, 两点.
两点.
(Ⅰ)若
 ,
, ,求
,求 的面积;
的面积;(Ⅱ)若直线
 过点
过点 ,证明:
,证明: 为定值,并求此定值.
为定值,并求此定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某企业生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间
 ,
, ,
, 内的频率之比为
内的频率之比为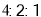 .
.
(Ⅰ)求这些产品质量指标值落在区间
 内的频率;
内的频率;(Ⅱ)用分层抽样的方法在区间
 内抽取一个容量为6的样本,将该样本看成一个总体,从中任意
内抽取一个容量为6的样本,将该样本看成一个总体,从中任意抽取2件产品,求这2件产品都在区间
 内的概率.
内的概率.
相关试题

