【题目】 用总长14.8米的钢条制作一个长方体容器的框架,如果所制容器底面一边的长比另一边的长多0.5米,那么高为多少时容器的容积最大?最大容积是多少?
参考答案:
【答案】x=1时,即h=1.2时,V取到最大值1.8
【解析】本试题主要是考查了导数在实际生活中的运用。首先设出变量设底面一边长为x,则另一边长为x+0.5,高为h,容积为V,然后利用体积的公式表示出函数,结合导数的思想来判定单调性,确定出最值。
注意实际问题中,一个极值就是最值。
设底面一边长为x,则另一边长为x+0.5,高为h,容积为V
则4x+4(x+0.5)+4h=14.8,得到 h=3.2-2x
V=x(x+0.5)h =x(x+0.5)(3.2-2x)=-2x3+2.2x2+1.6x (0<x<1.6)
由V’=0得x=1或![]()
![]()
![]()
所以,x=1时,即h=1.2时,V取到最大值1.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】从某企业生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间
 ,
, ,
, 内的频率之比为
内的频率之比为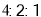 .
.
(Ⅰ)求这些产品质量指标值落在区间
 内的频率;
内的频率;(Ⅱ)用分层抽样的方法在区间
 内抽取一个容量为6的样本,将该样本看成一个总体,从中任意
内抽取一个容量为6的样本,将该样本看成一个总体,从中任意抽取2件产品,求这2件产品都在区间
 内的概率.
内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某几何体的三视图如下图,则该几何体的体积为( )
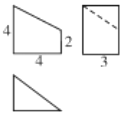
A. 18 B. 20 C. 24 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , 若4Sn=(2n﹣1)an+1+1,且a1=1.
(1)求数列{an}的通项公式;
(2)设cn=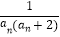 ,数列{cn}的前n项和为Tn .
,数列{cn}的前n项和为Tn .
①求Tn;
②对于任意的n∈N*及x∈R,不等式kx2﹣6kx+k+7+3Tn>0恒成立,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
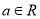 ,若
,若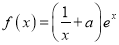 在区间
在区间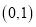 上有且只有一个极值点,则
上有且只有一个极值点,则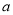 的取值范围是( )
的取值范围是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
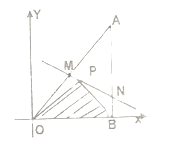
查看答案和解析>>【题目】如图所示,将一块直角三角形木板
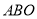 置于平面直角坐标系中,已知
置于平面直角坐标系中,已知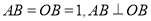 ,点
,点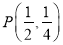 是三角形木板内一点,现因三角形木板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点
是三角形木板内一点,现因三角形木板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点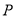 的任一直线
的任一直线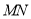 将三角形木板锯成
将三角形木板锯成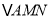 .设直线
.设直线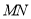 的斜率为
的斜率为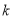 .
.
(Ⅰ)求点
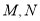 的坐标及直线
的坐标及直线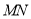 的斜率
的斜率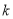 的范围;
的范围;(Ⅱ)令
 的面积为
的面积为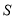 ,试求出
,试求出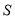 的取值范围;
的取值范围;(Ⅲ)令(Ⅱ)中
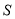 的取值范围为集合
的取值范围为集合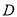 ,若
,若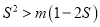 对
对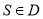 恒成立,求
恒成立,求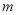 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}中,a1=1,a3=﹣3.
(1)求数列{an}的通项公式;
(2)若数列{an}的前k项和Sk=﹣35,求k的值.
相关试题

