【题目】某基建公司年初以100万元购进一辆挖掘机,以每年22万元的价格出租给工程队.基建公司负责挖掘机的维护,第一年维护费为2万元,随着机器磨损,以后每年的维护费比上一年多2万元,同时该机器第x(x∈N* , x≤16)年末可以以(80﹣5x)万元的价格出售.
(1)写出基建公司到第x年末所得总利润y(万元)关于x(年)的函数解析式,并求其最大值;
(2)为使经济效益最大化,即年平均利润最大,基建公司应在第几年末出售挖掘机?说明理由.
参考答案:
【答案】
(1)解:y=22x+(80﹣5x)﹣100﹣(2+4+…+2x)=﹣20+17x﹣ ![]() x(2+2x)
x(2+2x)
=﹣x2+16x﹣20=﹣(x﹣8)2+44(x≤16,x∈N),
由二次函数的性质可得,当x=8时,ymax=44,
即有总利润的最大值为44万元
(2)解:年平均利润为 ![]() =16﹣(x+
=16﹣(x+ ![]() ),设f(x)=16﹣(x+
),设f(x)=16﹣(x+ ![]() ),x>0,
),x>0,
由x+ ![]() ≥2
≥2 ![]() =4
=4 ![]() ,当x=2
,当x=2 ![]() 时,取得等号.
时,取得等号.
由于x为整数,且4<2 ![]() <5,f(4)=16﹣(4+5)=7,f(5)=7,
<5,f(4)=16﹣(4+5)=7,f(5)=7,
即有x=4或5时,f(x)取得最大值,且为7万元.
故使得年平均利润最大,基建公司应在第4或5年末出售挖掘机
【解析】(1)由题意可得总利润y等于总收入减去总成本(固定资产加上维护费),结合二次函数的最值求法,即可得到最大值;(2)求得年平均利润为 ![]() ,再由基本不等式,结合x为正整数,加上即可得到最大值,及对应的x的值.
,再由基本不等式,结合x为正整数,加上即可得到最大值,及对应的x的值.
-
科目: 来源: 题型:
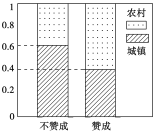
查看答案和解析>>【题目】某省高考改革实施方案指出:该省高考考生总成绩将由语文、数学、外语3门统一高考成绩和学生自主选择的学业水平等级性考试科目共同构成,该省教育厅为了解正在读高中的学生家长对高考改革方案所持的赞成态度,随机从中抽取了100名城乡家长作为样本进行调查,调查结果显示样本中有25人持不赞成意见,如图是根据样本的调查结果绘制的等高条形图.
(1)根据已知条件与等高条形图完成下面的
 列联表,并判断我们能否有95%的把握认为“赞成高考改革方案与城乡户口有关”?
列联表,并判断我们能否有95%的把握认为“赞成高考改革方案与城乡户口有关”?
注:
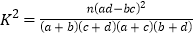 ,其中
,其中 .
.
(2)用样本的频率估计概率,若随机在全省不赞成高考改革的家长中抽取3个,记这3个家长中是城镇户口的人数为
 ,试求
,试求 的分布列及数学期望
的分布列及数学期望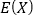 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(l)求
 的单调区间;
的单调区间;(2)若函数
 在区间
在区间 内存在唯一的极值点,求
内存在唯一的极值点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三棱柱ABC﹣A1B1C1的直观图和三视图如图所示,E是棱CC1上一点.

(1)若CE=2EC1 , 求三棱锥E﹣ACB1的体积.
(2)若E是CC1的中点,求C到平面AEB1的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=(ex﹣1)(x﹣1)k , k∈N* , 若函数y=f(x)在x=1处取到极小值,则k的最小值为( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是边长2的正方形,E,F分别为线段DD1 , BD的中点.
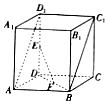
(1)求证:EF∥平面ABC1D1;
(2)AA1=2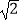 ,求异面直线EF与BC所成的角的大小.
,求异面直线EF与BC所成的角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业投资1千万元用于一个高科技项目,每年可获利25%.由于企业间竞争激烈,每年底需要从利润中取出资金200万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.经过多少年后,该项目的资金可以达到4倍的目标?
相关试题

