【题目】已知函数![]() .
.
(I)求函数![]() 的单调区间;
的单调区间;
(II)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(III)在(II)的条件下,对任意的![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(I)当![]() 时,
时,![]() 在
在![]() 上单调递增,无单调递减区间,当
上单调递增,无单调递减区间,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(II)
;(II)![]() ;(III)证明见解析.
;(III)证明见解析.
【解析】试题分析:(I)利用![]() 时
时![]() 为单调增函数,
为单调增函数,![]() 时
时![]() 为单调减函数这一性质来分情况讨论题中
为单调减函数这一性质来分情况讨论题中![]() 单调区间问题;(II)根据函数单调性与最值,若
单调区间问题;(II)根据函数单调性与最值,若![]() 在
在![]() 上恒成立,则函数的最大值小于或等于零.当
上恒成立,则函数的最大值小于或等于零.当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,说明
,说明![]() 时
时![]() ,不合题意舍去.当
,不合题意舍去.当![]() 时,
时,![]() 的最大值小于零.但
的最大值小于零.但![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 只能等于零.令
只能等于零.令![]() 即可求得答案;(III)首先将
即可求得答案;(III)首先将![]() 的表达式表达出来,化简转化为
的表达式表达出来,化简转化为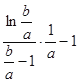 的形式,再根据(II)的结论得到
的形式,再根据(II)的结论得到![]() ,后逐步化简
,后逐步化简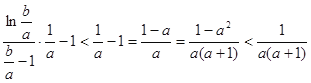 ,原命题得证.
,原命题得证.
试题解析:(I)![]() ,
,
当![]() 时,
时,![]() 恒成立,则函数
恒成立,则函数![]() 在
在![]() 上单调递增,无单调递减区间;
上单调递增,无单调递减区间;
当![]() 时,由
时,由![]() ,得
,得![]() ,由
,由![]() ,
,
得![]() ,此时
,此时![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(II)由(I)知:当![]() 时,
时,![]() 在
在![]() 上递增,
上递增,![]() ,显然不成立;
,显然不成立;
当![]() 时,
时,![]() ,只需
,只需![]() 即可,
即可,
令![]() ,则
,则![]() ,
,![]()
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
![]() .
.
![]() 对
对![]() 恒成立,也就是
恒成立,也就是![]() 对
对![]() 恒成立,
恒成立,
![]() ,解得
,解得![]() ,
,![]() 若
若![]() 在
在![]() 上恒成立,则
上恒成立,则![]() .
.
(III)证明: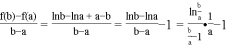 ,
,
由(II)得![]() 在
在![]() 上恒成立,即
上恒成立,即![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
又由![]() 得
得![]() ,所以有
,所以有![]() ,即
,即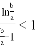 .
.
则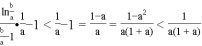 ,
,
则原不等式![]() 成立. ………(12分)
成立. ………(12分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
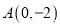 ,椭圆
,椭圆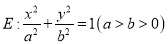 的离心率为
的离心率为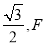 是椭圆的焦点,直线
是椭圆的焦点,直线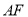 的斜率为
的斜率为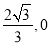 为坐标原点.
为坐标原点.(1)求椭圆
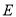 的方程;
的方程;(2)设过点
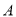 的直线
的直线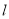 与椭圆
与椭圆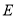 相交于
相交于 两点,当
两点,当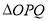 的面积最大时,求直线
的面积最大时,求直线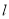 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
 中,平面
中,平面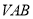
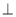 平面
平面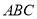 ,
, 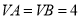 ,
, 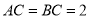 且
且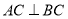 ,
, 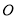 ,
, 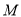 分别为
分别为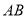 ,
, 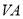 的中点.
的中点.(1)求证:
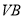
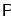 平面
平面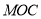 ;
;(2)求证:平面
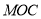
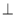 平面
平面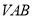 ;
;(3)求三棱锥
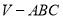 的体积.
的体积.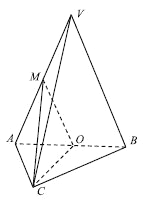
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为
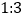 ,且成绩分布在
,且成绩分布在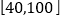 ,分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见下图)
,分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见下图)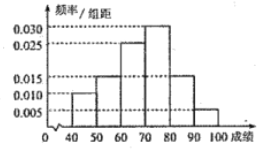
(Ⅰ)求所抽取样本的平均值
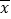 (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);(Ⅱ)填写下面的
 列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”?
列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”?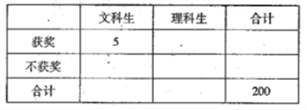
附表及公式:
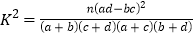 ,其中
,其中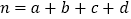
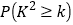
0.15
0.10
0.05
0.025
0.010
0.005
0.001
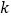
2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某智能手机制作完成之后还需要依次通过三道严格的审核程序,第一道审核、第二道审核、第三道审核通过的概率分别为
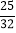 ,
, ,
, ,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.
,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.(1)求审核过程中只通过两道程序的概率;
(2)现有3部该智能手机进入审核,记这3部手机可以出厂销售的部数为
 ,求
,求 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比试验,甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在
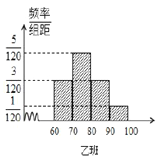
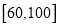 区间内(满分100分),并绘制频率分布直方图如图所示,两个班人数均为60人,成绩80分及以上为优良.
区间内(满分100分),并绘制频率分布直方图如图所示,两个班人数均为60人,成绩80分及以上为优良.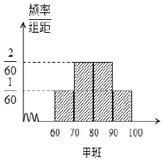
(1)根据以上信息填好
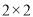 联表,并判断出有多大的把握认为学生成绩优良与班级有关?
联表,并判断出有多大的把握认为学生成绩优良与班级有关?(2)以班级分层抽样,抽取成绩优良的5人参加座谈,现从5人中随机选3人来作书面发言,求发言人至少有2人来自甲班的概率.
(以下临界值及公式仅供参考)
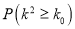
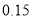
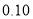
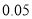
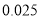
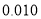
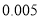
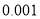
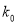
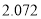
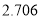
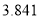
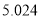
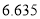
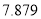
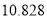
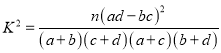 ,
, 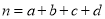 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】现安排甲乙丙丁戊5名学生分别担任语文、数学、英语、物理、化学学科的科代表,要求甲不当语文科代表,乙不当数学科代表,若丙当物理科代表则丁必须当化学科代表,则不同的选法共有多少种( )
A. 53 B. 67 C. 85 D. 91
相关试题

