【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见下图)
,分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见下图)
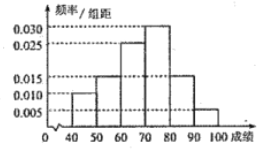
(Ⅰ)求所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)填写下面的![]() 列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”?
列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”?
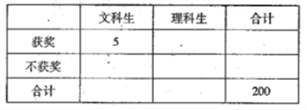
附表及公式:
![]() ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考答案:
【答案】(Ⅰ)40;(Ⅱ)答案见解析.
【解析】试题分析:(1)利用频率和为![]() ,求
,求![]() 的值,利用同一组中的数据用该组区间的中点值作代表,计算所抽取样本的平均值
的值,利用同一组中的数据用该组区间的中点值作代表,计算所抽取样本的平均值![]() ;〔2〕利用公式
;〔2〕利用公式![]() 求出
求出![]() 与临界值比较,即可得出结论.
与临界值比较,即可得出结论.
试题解析:(Ⅰ)![]()
![]() .
.
文科生参赛人数![]() (人)
(人)
理科生参赛人数![]() (人)
(人)
优秀学生数![]() (人)
(人)
(Ⅱ)
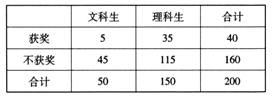
![]()
![]() ,
,
所以有超过95%的把握认为“获奖与学生的文理科有关”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了
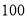 名观众进行调查,其中女性有
名观众进行调查,其中女性有 名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图: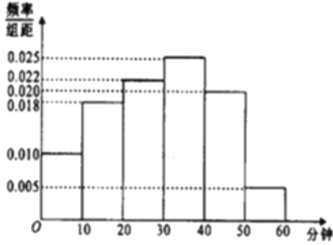
将日均收看该体育节目时间不低于
 分钟的观众称“体育述”,已知“体育迷”中
分钟的观众称“体育述”,已知“体育迷”中 名女性.
名女性.(1)根据已知条件完成下面的
 列联表,并据此资料你是否认为“体育迷”与性別有关?
列联表,并据此资料你是否认为“体育迷”与性別有关?非体育迷
体育迷
合计
男
女
合计
(2)将日均收看该体育项目不低于
 分钟的观众称为“超级体育迷”,已知“超级体育述”中有
分钟的观众称为“超级体育迷”,已知“超级体育述”中有 名女性,若从“超级体育述”中任意选取
名女性,若从“超级体育述”中任意选取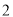 人,求至少有
人,求至少有 名女性观众的概率.
名女性观众的概率.附:
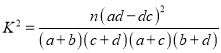 ,
,
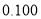
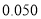

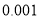
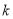
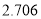
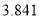
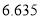
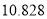
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
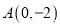 ,椭圆
,椭圆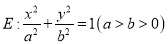 的离心率为
的离心率为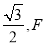 是椭圆的焦点,直线
是椭圆的焦点,直线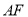 的斜率为
的斜率为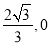 为坐标原点.
为坐标原点.(1)求椭圆
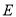 的方程;
的方程;(2)设过点
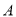 的直线
的直线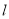 与椭圆
与椭圆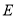 相交于
相交于 两点,当
两点,当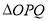 的面积最大时,求直线
的面积最大时,求直线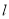 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
 中,平面
中,平面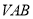
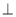 平面
平面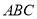 ,
, 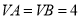 ,
, 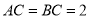 且
且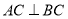 ,
, 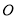 ,
, 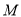 分别为
分别为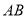 ,
, 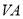 的中点.
的中点.(1)求证:
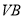
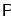 平面
平面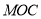 ;
;(2)求证:平面
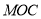
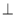 平面
平面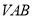 ;
;(3)求三棱锥
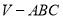 的体积.
的体积.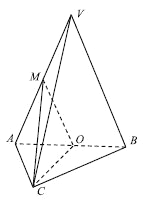
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
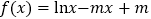 .
.(I)求函数
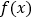 的单调区间;
的单调区间;(II)若
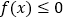 在
在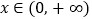 上恒成立,求实数
上恒成立,求实数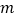 的取值范围;
的取值范围;(III)在(II)的条件下,对任意的
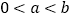 ,求证:
,求证: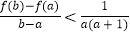 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某智能手机制作完成之后还需要依次通过三道严格的审核程序,第一道审核、第二道审核、第三道审核通过的概率分别为
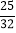 ,
, ,
, ,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.
,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.(1)求审核过程中只通过两道程序的概率;
(2)现有3部该智能手机进入审核,记这3部手机可以出厂销售的部数为
 ,求
,求 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
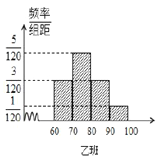
查看答案和解析>>【题目】某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比试验,甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在
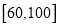 区间内(满分100分),并绘制频率分布直方图如图所示,两个班人数均为60人,成绩80分及以上为优良.
区间内(满分100分),并绘制频率分布直方图如图所示,两个班人数均为60人,成绩80分及以上为优良.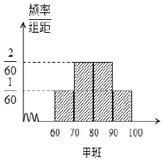
(1)根据以上信息填好
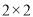 联表,并判断出有多大的把握认为学生成绩优良与班级有关?
联表,并判断出有多大的把握认为学生成绩优良与班级有关?(2)以班级分层抽样,抽取成绩优良的5人参加座谈,现从5人中随机选3人来作书面发言,求发言人至少有2人来自甲班的概率.
(以下临界值及公式仅供参考)
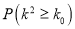
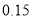
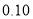
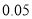
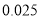
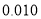
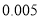
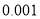
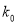
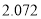
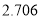
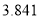
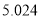
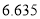
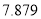
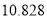
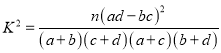 ,
, 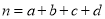 .
.
相关试题

