【题目】如图,已知双曲线C: ![]() =1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q,若∠PAQ=
=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q,若∠PAQ= ![]() ,且
,且 ![]() |,则双曲线C的离心率为( )
|,则双曲线C的离心率为( ) 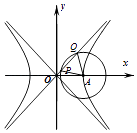
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】D
【解析】解:∵∠PAQ= ![]() ,AP=AQ, ∴△PAQ是等边三角形,
,AP=AQ, ∴△PAQ是等边三角形,
设圆A的半径为r,
过A作AB⊥PQ,垂足为B,则B为PQ的中点,
∴PB= ![]() r,AB=
r,AB= ![]() r,
r,
∵OQ=3OP,∴OB=2OP=r,
∴tan∠AOB= ![]() =
= ![]() ,
,
又渐近线方程为y= ![]() ,
,
∴ ![]() =
= ![]() ,即b=
,即b= ![]() a,
a,
∴e= ![]() =
= ![]() =
= ![]() ,
,
解法二:由于双曲线的离心率e>1,排除A,B,C,
故选D.
过A作AB⊥PQ,设圆A半径为r,三角形APQ是等边三角形,用r表示出OB,AB计算渐近线的斜率,从而得出a,b的关系得出离心率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P在直线x+3y﹣2=0上,点Q在直线x+3y+6=0上,线段PQ的中点为M(x0 , y0),且y0<x0+2,则
 的取值范围是( )
的取值范围是( )
A.[﹣ ,0)
,0)
B.(﹣ ,0)??
,0)??
C.(﹣ ,+∞)
,+∞)
D.(﹣∞,﹣ )∪(0,+∞)
)∪(0,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC
 BC,且AC=BC.
BC,且AC=BC.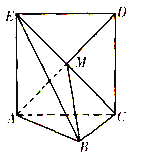
(1)求证:AM
 平面EBC;
平面EBC;(2)求直线AB与平面EBC所成角的大小,
(3)求二面角A-BE-C的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正三角形
 的边长为
的边长为 ,将它沿高
,将它沿高 翻折,使点
翻折,使点 与点
与点 间的距离为
间的距离为 ,此时四面体
,此时四面体 外接球表面积为
外接球表面积为A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,经过村庄A有两条夹角60°为的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M,N(异于村庄A),要求PM=PN=MN=2(单位:千米).记∠AMN=θ.

(1)将AN,AM用含θ的关系式表示出来;
(2)如何设计(即AN,AM为多长时),使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离AP最大)? -
科目: 来源: 题型:
查看答案和解析>>【题目】某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生 (I)分别求出按程序框图正确编程运行时输出y的值为i的概率pi(i=1,2,3);
(II)甲乙两同学依据自己对程序框图的理解,各自编程写出程序重复运行n次后,统计记录输出y的值为i(i=1,2,3)的频数,以下是甲乙所作频数统计表的部分数据.
甲的频数统计图(部分)运行次数n
输出y的值为1的频数
输出y的值为2的频数
输出y的值为3的频数
30
14
6
10
…
…
…
…
2100
1027
376
697
乙的频数统计图(部分)
运行次数n
输出y的值为1的频数
输出y的值为2的频数
输出y的值为3的频数
30
12
11
7
…
…
…
…
2100
1051
696
353
当n=2100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编程序符合要求的可能系较大;
(III)将按程序摆图正确编写的程序运行3次,求输出y的值为2的次数ξ的分布列及数学期望.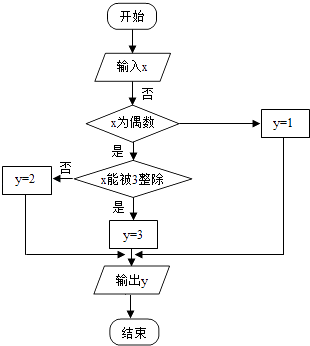
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P﹣ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.
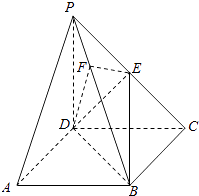
(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
(2)若面DEF与面ABCD所成二面角的大小为 ,求
,求  的值.
的值.
相关试题

