搜索
【题目】如图，正方形ACDE所在的平面与平面ABC垂直，M是CE和AD的交点，AC
BC,且AC=BC.
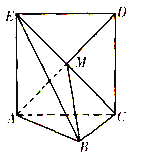
(1)求证：AM平面EBC；
(2)求直线AB与平面EBC所成角的大小，
(3)求二面角A-BE-C的大小.
参考答案：
【答案】（1）见解析（2）30°（3）60°
【解析】
(1)以点A为原点，以过A点平行于BC的直线为x轴，分别以直线AC和AE为y轴和z轴，建立空间直角坐标系A-xyz,利用向量法能证明
平面
(2)求出平面EBC的法向量，利用线面角公式求解(3)求平面EAB的法向量，根据向量法求出二面角A-BE-C的大小.
（1）如图所示：
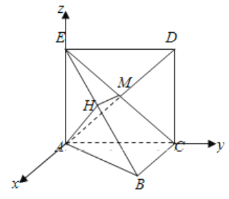
建立空间直角坐标系A-xy，设
，
则
所以
∴
，
，∴
，
.
∴平面.
（2）∵平面，∴
为平面的一个法向量，
∵
，∴
，∴
，
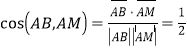∴直线
与平面所成的角的大小为30°.
（3）面
的法向量为
，面
的法向量为
，
∴
故二面角
的大小为60°
-
科目： 来源： 题型：
查看答案和解析>>【题目】将函数
的图象向左平移 
个单位长度后，所得函数g（x）的图象关于原点对称，则函数f（x）在 
的最大值为（ ）
A.0
B.
C.
D.1 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知点A（0，0），若函数f（x）的图象上存在两点B、C到点A的距离相等，则称该函数f（x）为“点距函数”，给定下列三个函数：①y=﹣x+2；②
；③y=x+1．其中，“点距函数”的个数是（ ）
A.0
B.1
C.2
D.3 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知点P在直线x+3y﹣2=0上，点Q在直线x+3y+6=0上，线段PQ的中点为M（x0 ， y0），且y0＜x0+2，则
的取值范围是（ ）
A.[﹣
，0）
B.（﹣ ，0）??
C.（﹣ ，+∞）
D.（﹣∞，﹣ ）∪（0，+∞） -
科目： 来源： 题型：
查看答案和解析>>【题目】正三角形
的边长为
,将它沿高
翻折,使点
与点
间的距离为
,此时四面体
外接球表面积为A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知双曲线C：
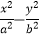=1（a＞0，b＞0）的右顶点为A，O为坐标原点，以A为圆心的圆与双曲线C的某渐近线交于两点P，Q，若∠PAQ= 
，且 
|，则双曲线C的离心率为（ ）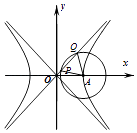 
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，经过村庄A有两条夹角60°为的公路AB，AC，根据规划拟在两条公路之间的区域内建一工厂P，分别在两条公路边上建两个仓库M，N（异于村庄A），要求PM=PN=MN=2（单位：千米）．记∠AMN=θ．
（1）将AN，AM用含θ的关系式表示出来；
（2）如何设计（即AN，AM为多长时），使得工厂产生的噪声对居民的影响最小（即工厂与村庄的距离AP最大）？
相关试题
