【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过原点的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 不是椭圆
不是椭圆![]() 的顶点),点
的顶点),点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() .直线
.直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.设直线
两点.设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,证明存在常数
,证明存在常数![]() 使得
使得![]() ,并求出
,并求出![]() 的值.
的值.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)甶椭圆离心率得到![]() 的关系,化简椭圆方程,和直线方程联立后求出交点的横坐标,把弦长用交点横坐标表示,则
的关系,化简椭圆方程,和直线方程联立后求出交点的横坐标,把弦长用交点横坐标表示,则![]() 的值可求,进一步得到
的值可求,进一步得到![]() 的值,则椭圆方程可求;(2)设出
的值,则椭圆方程可求;(2)设出![]() 的坐标分别为
的坐标分别为![]() 用
用![]() 的坐标表示
的坐标表示![]() 的坐标,把
的坐标,把![]() 和
和![]() 的斜率都用
的斜率都用![]() 的坐标表示,写出直线
的坐标表示,写出直线![]() 的方程,和椭圆方程联立后利用根与系数关系得到
的方程,和椭圆方程联立后利用根与系数关系得到![]() 横纵坐标的和,求出
横纵坐标的和,求出![]() 中点坐标,则
中点坐标,则![]() 斜率可求,再写出
斜率可求,再写出![]() 所在直线方程,取
所在直线方程,取![]() 得到
得到![]() 点坐标,由两点求斜率得到
点坐标,由两点求斜率得到![]() 的斜率,由两直线斜率的关系得到
的斜率,由两直线斜率的关系得到![]() 的值;
的值;
试题解析:(Ⅰ)∵![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() .①
.①
设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,不妨设点
两点,不妨设点![]() 为第一象限内的交点.∴
为第一象限内的交点.∴![]() ,∴
,∴![]() 代入椭圆方程可得
代入椭圆方程可得![]() .②
.②
由①②知![]() ,
,![]() ,所以椭圆的方程为:
,所以椭圆的方程为:![]() .
.
(Ⅱ)设![]()
![]() ,则
,则![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,又
,又![]() ,故直线
,故直线![]() 的斜率为
的斜率为![]() .设直线
.设直线![]() 的方程为
的方程为![]() ,由题知
,由题知
![]() ,
,![]() 联立
联立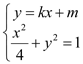 ,得
,得![]()
![]() .
.
∴![]() ,
,![]()
![]() ,由题意知
,由题意知![]() ,
,
∴![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
令![]() ,得
,得![]() ,即
,即![]() ,可得
,可得![]()
![]() ,∴
,∴![]() ,即
,即![]() .
.
因此存在常数![]() 使得结论成立.
使得结论成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直三棱柱
 中,
中, ,
, ,
, ,
, ,点
,点 在线段
在线段 上.
上.
(Ⅰ)证明
 ;
;(Ⅱ)若
 是
是 中点,证明
中点,证明 平面
平面 ;
;(Ⅲ)当
 时,求二面角
时,求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名篮球运动员互不影响地在同一位置投球,命中率分别为
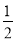 与
与 ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为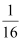 。
。(1)求乙投球的命中率
 。
。(2)若甲投球1次,乙投球2次,两人共命中的次数记为
 ,求
,求 的分布列和数学期望。
的分布列和数学期望。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:x2+y2-2x+4y-4=0,
(1)求圆C关于直线
 对称的圆的方程;
对称的圆的方程;(2)问是否存在斜率为1的直线l,使l被圆C截得弦AB,且以AB为直径的圆经过点
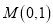 ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】身穿红、黄两种颜色衣服的各有两人,身穿蓝颜色衣服的有一人,现将这五人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法共有( )
A. 24种 B. 28种 C. 36种 D. 48种
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
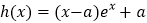 .
.(1)若
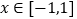 ,求函数
,求函数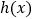 的最小值;
的最小值;(2)当
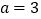 时,若对
时,若对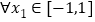 ,
,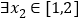 ,使得
,使得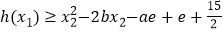 成立,求
成立,求 的范围.
的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
相关试题

