【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上.
上.

(Ⅰ)证明![]() ;
;
(Ⅱ)若![]() 是
是![]() 中点,证明
中点,证明![]() 平面
平面![]() ;
;
(Ⅲ)当![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(1)见解析(2)![]()
【解析】试题分析:以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() ,(Ⅰ)分别求出向量
,(Ⅰ)分别求出向量![]() 的坐标根据
的坐标根据![]() 可得结果;(Ⅱ)求出平面
可得结果;(Ⅱ)求出平面![]() 的法向量,利用向量法能证明
的法向量,利用向量法能证明![]() 平面
平面![]() ;(Ⅲ)求出平面
;(Ⅲ)求出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,利用空间向量法夹角余弦公式能求出二面角
的法向量,利用空间向量法夹角余弦公式能求出二面角![]() 的余弦值.
的余弦值.
试题解析:(Ⅰ)证明:如图,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() .则
.则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() ,所以
,所以![]() .
.

(Ⅱ)解法一:

![]()
设平面![]() 的法向量
的法向量![]() ,
,
由![]()
![]() ,
,
且![]()
![]() ,
,
令![]() 得
得![]() ,
,
所以![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;
;
解法二:证明:连接![]() ,交
,交![]() 于
于![]() ,
,![]() .
.
因为直三棱柱![]() ,
,![]() 是
是![]() 中点,
中点,
所以侧面![]() 为矩形,
为矩形,![]() 为
为![]() 的中位线.
的中位线.
所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅲ)由(Ⅰ)知![]() ,
,
设![]() ,
,
因为点![]() 在线段
在线段![]() 上,且
上,且![]() ,即
,即![]()
![]()
![]() .
.
所以![]() ,
,![]() ,
,![]()
![]() .
.
所以![]() ,
,![]() .
.
平面![]() 的法向量为
的法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由![]() ,
,![]() ,得
,得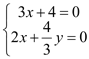 ,
,
所以![]() ,
,![]() ,
,![]()
![]() .
.
设二面角![]() 的大小为
的大小为![]() ,
,
所以 .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
设函数
 ,
, .
.(Ⅰ)当
 时,求函数
时,求函数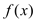 的极小值;
的极小值;(Ⅱ)讨论函数
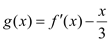 零点的个数;
零点的个数;(Ⅲ)若对任意的
 ,
,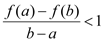 恒成立,求
恒成立,求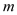 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
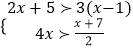 .
. -
科目: 来源: 题型:
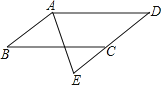
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E.求证:DA=DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名篮球运动员互不影响地在同一位置投球,命中率分别为
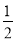 与
与 ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为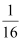 。
。(1)求乙投球的命中率
 。
。(2)若甲投球1次,乙投球2次,两人共命中的次数记为
 ,求
,求 的分布列和数学期望。
的分布列和数学期望。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:x2+y2-2x+4y-4=0,
(1)求圆C关于直线
 对称的圆的方程;
对称的圆的方程;(2)问是否存在斜率为1的直线l,使l被圆C截得弦AB,且以AB为直径的圆经过点
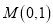 ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,椭圆
中,椭圆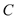 :
: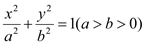 的离心率为
的离心率为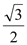 ,直线
,直线 被椭圆
被椭圆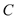 截得的线段长为
截得的线段长为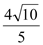 .
.(Ⅰ)求椭圆
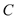 的方程;
的方程;(Ⅱ)过原点的直线与椭圆
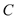 交于
交于 ,
,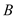 两点(
两点( ,
,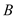 不是椭圆
不是椭圆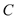 的顶点),点
的顶点),点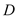 在椭圆
在椭圆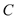 上,且
上,且 .直线
.直线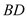 与
与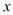 轴、
轴、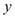 轴分别交于
轴分别交于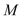 ,
,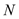 两点.设直线
两点.设直线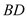 ,
,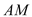 的斜率分别为
的斜率分别为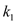 ,
,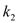 ,证明存在常数
,证明存在常数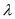 使得
使得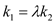 ,并求出
,并求出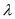 的值.
的值.
相关试题

