【题目】身穿红、黄两种颜色衣服的各有两人,身穿蓝颜色衣服的有一人,现将这五人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法共有( )
A. 24种 B. 28种 C. 36种 D. 48种
参考答案:
【答案】D
【解析】试题分析:由题意知先使五个人的全排列,共有A55种结果,去掉相同颜色衣服的人都相邻的情况,再去掉仅穿蓝色衣服的人的相邻和仅穿穿黄色衣服的人相邻两种情况,从而求得结果.
由题意知先使五个人的全排列,共有![]() 种结果.
种结果.
去掉同颜色衣服相的人都相邻的情况,再去掉仅穿蓝色相邻和仅穿黄色相邻的两种情况.
穿相同颜色衣服的人都相邻的情况有![]() 种(相邻的看成一整体),
种(相邻的看成一整体),
当穿兰色衣服的相邻,而穿黄色衣服的人不相邻,共有![]() 种(相邻的看成一整体,不相邻利用插空法),同理当穿黄色衣服的相邻,而穿兰色衣服的人不相邻,也共有
种(相邻的看成一整体,不相邻利用插空法),同理当穿黄色衣服的相邻,而穿兰色衣服的人不相邻,也共有![]() 种,
种,
∴穿相同颜色衣服的人不能相邻的排法是![]() -
-![]() -2
-2![]() =48,
=48,
故答案 D
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名篮球运动员互不影响地在同一位置投球,命中率分别为
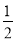 与
与 ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为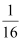 。
。(1)求乙投球的命中率
 。
。(2)若甲投球1次,乙投球2次,两人共命中的次数记为
 ,求
,求 的分布列和数学期望。
的分布列和数学期望。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:x2+y2-2x+4y-4=0,
(1)求圆C关于直线
 对称的圆的方程;
对称的圆的方程;(2)问是否存在斜率为1的直线l,使l被圆C截得弦AB,且以AB为直径的圆经过点
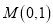 ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,椭圆
中,椭圆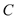 :
: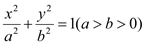 的离心率为
的离心率为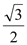 ,直线
,直线 被椭圆
被椭圆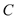 截得的线段长为
截得的线段长为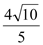 .
.(Ⅰ)求椭圆
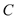 的方程;
的方程;(Ⅱ)过原点的直线与椭圆
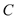 交于
交于 ,
,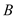 两点(
两点( ,
,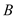 不是椭圆
不是椭圆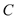 的顶点),点
的顶点),点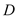 在椭圆
在椭圆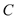 上,且
上,且 .直线
.直线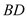 与
与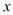 轴、
轴、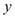 轴分别交于
轴分别交于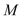 ,
,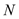 两点.设直线
两点.设直线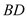 ,
,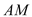 的斜率分别为
的斜率分别为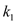 ,
,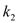 ,证明存在常数
,证明存在常数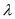 使得
使得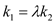 ,并求出
,并求出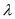 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
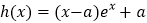 .
.(1)若
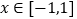 ,求函数
,求函数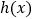 的最小值;
的最小值;(2)当
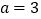 时,若对
时,若对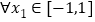 ,
,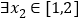 ,使得
,使得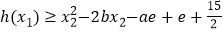 成立,求
成立,求 的范围.
的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根. -
科目: 来源: 题型:
查看答案和解析>>【题目】按照国家环保部发布的新修订的《环境空气质量标准》,规定:PM2.5的年平均浓度不得超过35微克/立方米,国家环保部门在2016年10月1日到2017年1月30日这120天对全国的PM2.5平均浓度的监测数据统计如下:
组别
PM2.5浓度(微克/立方米)
频数(天)
第一组
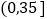
32
第二组
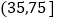
64
第三组
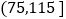
16
第四组
115以上
8
(1)在这120天中抽取30天的数据做进一步分析,每一组应抽取多少天?
(2)在(1)中所抽取的样本PM2.5的平均浓度超过75(微克/立方米)的若干天中,随机抽取2天,求恰好有一天平均浓度超过115(微克/立方米)的概率.
相关试题

