【题目】甲、乙两名篮球运动员互不影响地在同一位置投球,命中率分别为![]() 与
与![]() ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为![]() 。
。
(1)求乙投球的命中率![]() 。
。
(2)若甲投球1次,乙投球2次,两人共命中的次数记为![]() ,求
,求![]() 的分布列和数学期望。
的分布列和数学期望。
参考答案:
【答案】(1)乙投球的命中率为![]() (2)
(2)![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() 的数学期望
的数学期望![]()
【解析】本题考查离散型随机变量的分布列和期望,考查等可能事件的概率,考查对立事件的概率,是一个综合题,是近几年高考题目中经常出现的一个问题.
(Ⅰ)根据乙投球2次均未命中的概率为![]() ,两次是否投中相互之间没有影响,根据相互独立事件的概率公式写出乙两次都未投中的概率,列出方程,解方程即可.
,两次是否投中相互之间没有影响,根据相互独立事件的概率公式写出乙两次都未投中的概率,列出方程,解方程即可.
(II)做出甲投球命中的概率和乙投球命中的概率,因为两人共命中的次数记为ξ,得到变量可能的取值,看清楚变量对应的事件,做出事件的概率,写出分布列和期望
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
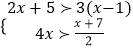 .
. -
科目: 来源: 题型:
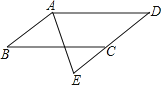
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E.求证:DA=DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直三棱柱
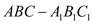 中,
中, ,
, ,
, ,
, ,点
,点 在线段
在线段 上.
上.
(Ⅰ)证明
 ;
;(Ⅱ)若
 是
是 中点,证明
中点,证明 平面
平面 ;
;(Ⅲ)当
 时,求二面角
时,求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:x2+y2-2x+4y-4=0,
(1)求圆C关于直线
 对称的圆的方程;
对称的圆的方程;(2)问是否存在斜率为1的直线l,使l被圆C截得弦AB,且以AB为直径的圆经过点
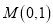 ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,椭圆
中,椭圆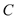 :
: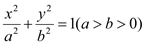 的离心率为
的离心率为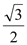 ,直线
,直线 被椭圆
被椭圆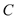 截得的线段长为
截得的线段长为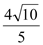 .
.(Ⅰ)求椭圆
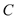 的方程;
的方程;(Ⅱ)过原点的直线与椭圆
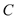 交于
交于 ,
,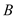 两点(
两点( ,
,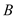 不是椭圆
不是椭圆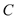 的顶点),点
的顶点),点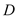 在椭圆
在椭圆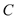 上,且
上,且 .直线
.直线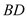 与
与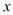 轴、
轴、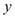 轴分别交于
轴分别交于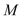 ,
,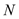 两点.设直线
两点.设直线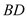 ,
,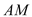 的斜率分别为
的斜率分别为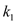 ,
,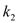 ,证明存在常数
,证明存在常数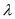 使得
使得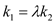 ,并求出
,并求出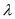 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】身穿红、黄两种颜色衣服的各有两人,身穿蓝颜色衣服的有一人,现将这五人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法共有( )
A. 24种 B. 28种 C. 36种 D. 48种
相关试题

