【题目】(12分)如图,底面是正三角形的直三棱柱![]() 中,D是BC的中点,
中,D是BC的中点,![]() .
.
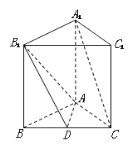
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求的A1 到平面![]() 的距离.
的距离.
参考答案:
【答案】(Ⅰ)参考解析,(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)需证明![]() 平面
平面![]() ,只需要在平面
,只需要在平面![]() 上找到一条直线与
上找到一条直线与![]() 平行,通过三角形的中位线可得以上结论.
平行,通过三角形的中位线可得以上结论.
(Ⅱ)需求点到面的距离,本题通过构建一个三棱锥,让其体积算两次即得到一个等式,即可取出结论.解法一通过三棱锥![]() 与三棱锥
与三棱锥![]() 的体积相等,由体积公式即可求得结论;解法二由(Ⅰ)得到的线面平行转化为三棱锥
的体积相等,由体积公式即可求得结论;解法二由(Ⅰ)得到的线面平行转化为三棱锥![]() 与三棱锥
与三棱锥![]() 体积相等,从而得到结论.
体积相等,从而得到结论.
试题解析:(1)连接![]() 交
交![]() 于O,连接OD,在
于O,连接OD,在![]() 中,O为
中,O为![]() 中点,D为BC中点
中点,D为BC中点
![]() 3分
3分
![]()
![]() 6分
6分

(2)解法一:设![]() 点到平面
点到平面![]() 的距离为h
的距离为h
在![]() 中,
中,![]()
![]()
![]()
![]() 为
为![]()
![]() 8分
8分
![]()
过D作![]() 于H
于H
又![]() 为直棱柱
为直棱柱
![]()
![]() 且
且![]() 10分
10分
![]()
即![]()
解得![]() 12分
12分
解法二:由①可知![]()
![]() 点
点![]() 到平面
到平面![]() 的距离等于点C到平面
的距离等于点C到平面![]() 的距离 8分
的距离 8分
![]() 为
为![]()
![]()
![]() 10分
10分
设点C到面![]() 的距离为h
的距离为h
![]()
即![]()
解得![]() 12分
12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A、B,要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
产品A(件)
产品B(件)
研制成本、搭载费用之和(万元)
20
30
计划最大资金额300万元
产品重量(千克)
10
5
最大搭载重量110千克
预计收益(万元)
80
60
试问:如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方体ABCD﹣A1B1C1D1 , 则过点A与AB、BC、CC1所成角均相等的直线有( )
A.1条
B.2条
C.4条
D.无数条 -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A、B、C所对的边分别为a、b、c,且BC边上的高为
 ,则当
,则当 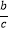 +
+  取得最大值时,内角A=( )
取得最大值时,内角A=( )
A.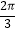
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把边长为2的正方形ABCD沿对角线BD折起并连接AC形成三棱锥C﹣ABD,其正视图、俯视图均为等腰直角三角形(如图所示),则三棱锥C﹣ABD的表面积为 .
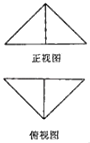
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A、B、C所对的边分别为a、b、c,a=
 .
.
(1)求bcosC+ccosB的值;
(2)若cosA= ,求b+c的最大值.
,求b+c的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名运动员的5次测试成绩如下图所示:
甲
茎
乙
5 7
1
6 8
8 8 2
2
3 6 7
设s1 , s2分别表示甲、乙两名运动员测试成绩的标准差,
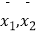 分别表示甲、乙两名运动员测试成绩的平均数,则有( )
分别表示甲、乙两名运动员测试成绩的平均数,则有( )
A. ,s1<s2
,s1<s2
B. ,s1>s2
,s1>s2
C. ,s1>s2
,s1>s2
D. ,s1=s2
,s1=s2
相关试题

