【题目】在△ABC中,内角A、B、C所对的边分别为a、b、c,且BC边上的高为 ![]() ,则当
,则当 ![]() +
+ ![]() 取得最大值时,内角A=( )
取得最大值时,内角A=( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】D
【解析】解:由三角形的面积公式可得,![]() bcsinA=
bcsinA= ![]() a
a ![]() ,
,
即a2=2bcsinA,
由余弦定理可得,a2=b2+c2﹣2bccosA,
可得b2+c2﹣2bccosA=2bcsinA,
即有 ![]() +
+ ![]() =2(sinA+cosA)
=2(sinA+cosA)
=2 ![]() (
( ![]() sinA+
sinA+ ![]() cosA)
cosA)
=2 ![]() sin(A+
sin(A+ ![]() ),
),
当A+ ![]() =
= ![]() ,即A=
,即A= ![]() 时,
时, ![]() +
+ ![]() 取得最大值2
取得最大值2 ![]() .
.
故选:D.
【考点精析】认真审题,首先需要了解基本不等式(基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() ),还要掌握正弦定理的定义(正弦定理:
),还要掌握正弦定理的定义(正弦定理:![]() )的相关知识才是答题的关键.
)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的方程为
 :
: 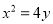 ,过点
,过点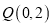 的一条直线与抛物线
的一条直线与抛物线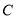 交于
交于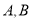 两点,若抛物线在
两点,若抛物线在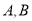 两点的切线交于点
两点的切线交于点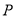 .
.(1)求点
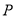 的轨迹方程;
的轨迹方程;(2)设直线
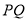 的斜率存在,取为
的斜率存在,取为 ,取直线
,取直线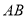 的斜率为
的斜率为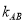 ,请验证
,请验证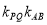 是否为定值?若是,计算出该值;若不是,请说明理由.
是否为定值?若是,计算出该值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A、B,要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
产品A(件)
产品B(件)
研制成本、搭载费用之和(万元)
20
30
计划最大资金额300万元
产品重量(千克)
10
5
最大搭载重量110千克
预计收益(万元)
80
60
试问:如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方体ABCD﹣A1B1C1D1 , 则过点A与AB、BC、CC1所成角均相等的直线有( )
A.1条
B.2条
C.4条
D.无数条 -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,底面是正三角形的直三棱柱
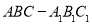 中,D是BC的中点,
中,D是BC的中点,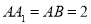 .
.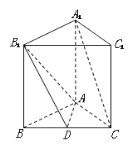
(Ⅰ)求证:
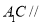 平面
平面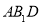 ;
;(Ⅱ)求的A1 到平面
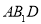 的距离.
的距离. -
科目: 来源: 题型:
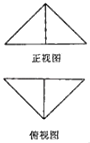
查看答案和解析>>【题目】把边长为2的正方形ABCD沿对角线BD折起并连接AC形成三棱锥C﹣ABD,其正视图、俯视图均为等腰直角三角形(如图所示),则三棱锥C﹣ABD的表面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A、B、C所对的边分别为a、b、c,a=
 .
.
(1)求bcosC+ccosB的值;
(2)若cosA= ,求b+c的最大值.
,求b+c的最大值.
相关试题

