【题目】在△ABC中,内角A、B、C所对的边分别为a、b、c,a= ![]() .
.
(1)求bcosC+ccosB的值;
(2)若cosA= ![]() ,求b+c的最大值.
,求b+c的最大值.
参考答案:
【答案】
(1)解:△ABC中,bcosC+ccosB=b ![]() +c
+c ![]() =a=
=a= ![]() ,
,
(2)解:若cosA= ![]() ,则A=
,则A= ![]() ,由余弦定理可得a2=3=b2+c2﹣2bccosA=(b+c)2﹣3bc,
,由余弦定理可得a2=3=b2+c2﹣2bccosA=(b+c)2﹣3bc,
∴(b+c)2=3+3bc≤3+3 ![]() ,∴b+c≤2
,∴b+c≤2 ![]() ,当且仅当b=c时,取等号,故b+c的最大值为2
,当且仅当b=c时,取等号,故b+c的最大值为2 ![]() .
.
【解析】(1)利用余弦定理求得bcosC+ccosB的值.(2)若cosA= ![]() ,利用余弦定理以及基本不等式求得b+c的最大值.
,利用余弦定理以及基本不等式求得b+c的最大值.
【考点精析】本题主要考查了余弦定理的定义的相关知识点,需要掌握余弦定理:![]() ;
;![]() ;
;![]() 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A、B、C所对的边分别为a、b、c,且BC边上的高为
 ,则当
,则当 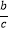 +
+  取得最大值时,内角A=( )
取得最大值时,内角A=( )
A.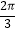
B.
C.
D.
-
科目: 来源: 题型:
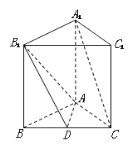
查看答案和解析>>【题目】(12分)如图,底面是正三角形的直三棱柱
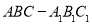 中,D是BC的中点,
中,D是BC的中点,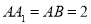 .
.
(Ⅰ)求证:
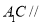 平面
平面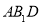 ;
;(Ⅱ)求的A1 到平面
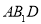 的距离.
的距离. -
科目: 来源: 题型:
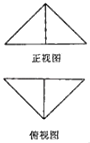
查看答案和解析>>【题目】把边长为2的正方形ABCD沿对角线BD折起并连接AC形成三棱锥C﹣ABD,其正视图、俯视图均为等腰直角三角形(如图所示),则三棱锥C﹣ABD的表面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名运动员的5次测试成绩如下图所示:
甲
茎
乙
5 7
1
6 8
8 8 2
2
3 6 7
设s1 , s2分别表示甲、乙两名运动员测试成绩的标准差,
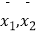 分别表示甲、乙两名运动员测试成绩的平均数,则有( )
分别表示甲、乙两名运动员测试成绩的平均数,则有( )
A. ,s1<s2
,s1<s2
B. ,s1>s2
,s1>s2
C. ,s1>s2
,s1>s2
D. ,s1=s2
,s1=s2 -
科目: 来源: 题型:
查看答案和解析>>【题目】20名同学参加某次数学考试成绩(单位:分)的频率分布直方图如下:
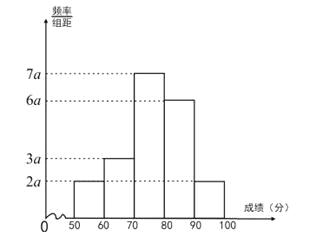
(Ⅰ)求频率分布直方图中
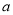 的值;
的值;(Ⅱ)分别求出成绩落在
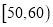 ,
, 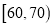 中的学生人数;
中的学生人数;(Ⅲ)从成绩在
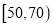 的学生中任选2人,求此2人的成绩都在
的学生中任选2人,求此2人的成绩都在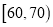 中的概率.
中的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆 的方程为
的方程为 .
.(1)求圆
 的直角坐标方程;
的直角坐标方程;(2)设圆
 与直线
与直线 交于点
交于点 ,若点
,若点 的坐标为
的坐标为 ,求
,求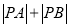 的最小值.
的最小值.
相关试题

