【题目】某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A、B,要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
产品A(件) | 产品B(件) | ||
研制成本、搭载费用之和(万元) | 20 | 30 | 计划最大资金额300万元 |
产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
预计收益(万元) | 80 | 60 |
试问:如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
参考答案:
【答案】解:设搭载产品Ax件,产品By件,
预计总收益z=80x+60y.
则  ,作出可行域,如图.
,作出可行域,如图.
作出直线l0:4x+3y=0并平移,由图象得,当直线经过M点时z能取得最大值, ![]() ,
,
解得 ![]() ,即M(9,4).
,即M(9,4).
所以zmax=80×9+60×4=960(万元).
答:搭载产品A9件,产品B4件,可使得总预计收益最大,为960万元.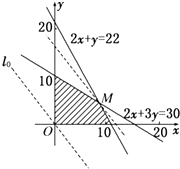
【解析】我们可以设搭载的产品中A有x件,产品B有y件,我们不难得到关于x,y的不等式组,即约束条件和目标函数,然后根据线行规划的方法不难得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
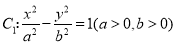 ,抛物线
,抛物线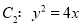 ,
, 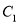 与
与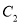 有公共的焦点
有公共的焦点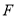 ,
, 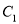 与
与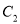 在第一象限的公共点为
在第一象限的公共点为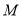 ,直线
,直线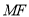 的倾斜角为
的倾斜角为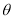 ,且
,且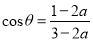 ,则关于双曲线的离心率的说法正确的是()
,则关于双曲线的离心率的说法正确的是()A. 仅有两个不同的离心率
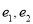 且
且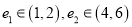 B. 仅有两个不同的离心率
B. 仅有两个不同的离心率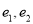 且
且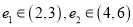 C. 仅有一个离心率
C. 仅有一个离心率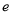 且
且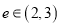 D. 仅有一个离心率
D. 仅有一个离心率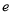 且
且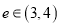
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68),再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
组号
分组
回答正确的人数
回答正确的人数占本组的比例
第1组
[18,28)
5
0.5
第2组
[28,38)
18
a
第3组
[38,48)
27
0.9
第4组
[48,58)
x
0.36
第5组
[58,68)
3
0.2
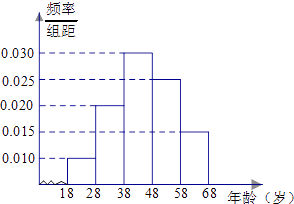
(1)分别求出a,x的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的方程为
 :
: 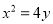 ,过点
,过点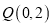 的一条直线与抛物线
的一条直线与抛物线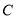 交于
交于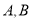 两点,若抛物线在
两点,若抛物线在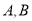 两点的切线交于点
两点的切线交于点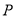 .
.(1)求点
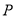 的轨迹方程;
的轨迹方程;(2)设直线
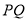 的斜率存在,取为
的斜率存在,取为 ,取直线
,取直线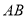 的斜率为
的斜率为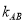 ,请验证
,请验证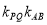 是否为定值?若是,计算出该值;若不是,请说明理由.
是否为定值?若是,计算出该值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方体ABCD﹣A1B1C1D1 , 则过点A与AB、BC、CC1所成角均相等的直线有( )
A.1条
B.2条
C.4条
D.无数条 -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A、B、C所对的边分别为a、b、c,且BC边上的高为
 ,则当
,则当 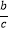 +
+  取得最大值时,内角A=( )
取得最大值时,内角A=( )
A.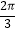
B.
C.
D.
-
科目: 来源: 题型:
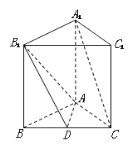
查看答案和解析>>【题目】(12分)如图,底面是正三角形的直三棱柱
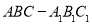 中,D是BC的中点,
中,D是BC的中点,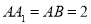 .
.
(Ⅰ)求证:
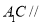 平面
平面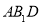 ;
;(Ⅱ)求的A1 到平面
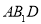 的距离.
的距离.
相关试题

