【题目】直三棱柱![]() 中,
中, ![]()
![]() 分别是
分别是![]() 的中点, 且
的中点, 且![]() ,
,
(1)证明: ![]() .
.
(2)棱![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() 若存在,说明点
若存在,说明点![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
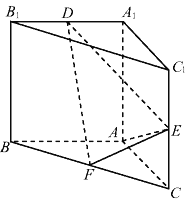
参考答案:
【答案】(1)见解析(2)点D为A1B1中点
【解析】试题分析:(1)由直三棱柱性质可得AB⊥AA1,根据条件![]() 可得AB⊥AE.最后根据线面垂直判定定理证明结论(2)研究二面角大小一般利用空间向量数量积,即先建立空间直角坐标系,设立各点坐标,利用方程组解各面法向量,再根据向量数量积求法向量夹角,根据法向量夹角与二面角关系建立方程,解出点
可得AB⊥AE.最后根据线面垂直判定定理证明结论(2)研究二面角大小一般利用空间向量数量积,即先建立空间直角坐标系,设立各点坐标,利用方程组解各面法向量,再根据向量数量积求法向量夹角,根据法向量夹角与二面角关系建立方程,解出点![]() 的坐标,确定其位置
的坐标,确定其位置
试题解析:(1)∵AE⊥A1B1,A1B1∥AB,
∴AB⊥AE.
又∵AB⊥AA1,AE∩AA1=A,
∴AB⊥平面A1ACC1.
(2) ∵ AB⊥平面A1ACC1.
又∵AC平面A1ACC1,
∴AB⊥AC.
以A为原点建立如图所示的空间直角坐标系Axyz.
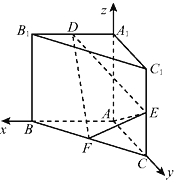
则A(0,0,0),E![]() ,F
,F![]()
![]() ,0
,0![]() ,A1(0,0,1),B1(1,0,1).
,A1(0,0,1),B1(1,0,1).
假设存在,![]() =λ
=λ![]() ,且λ∈[0,1],
,且λ∈[0,1],
∴D(λ,0,1).
设平面DEF的法向量为n=(x,y,z),
则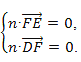
∵![]() ,
,
∴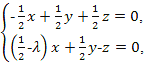
即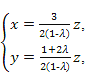
令z=2(1-λ),
∴n=(3,1+2λ,2(1-λ)).
由题可知平面ABC的一个法向量m=(0,0,1).
∵平面DEF与平面ABC所成锐二面角的余弦值为![]() ,
,
∴|cos(m,n)|= ,
,
即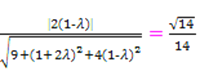 .
.
∴λ=![]() 或λ=
或λ=![]() (舍),
(舍),
∴当点D为A1B1中点时,满足要求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
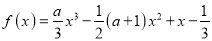 (
(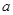
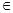 R).
R).(1) 若
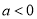 ,求函数
,求函数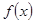 的极值;
的极值;(2)是否存在实数
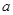 使得函数
使得函数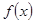 在区间
在区间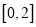 上有两个零点,若存在,求出
上有两个零点,若存在,求出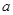 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
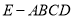 中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.(1)求
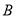 到平面
到平面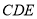 的距离
的距离(2)在线段
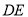 上是否存在一点
上是否存在一点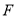 ,使
,使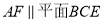 ?若存在,求出
?若存在,求出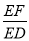 的值;若不存在,说明理由.
的值;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】f(x)是定义在R上的奇函数,对x,y∈R都有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,f(-1)=2.
(1)求证:f(x)为奇函数;
(2)求证:f(x)是R上的减函数;
(3)求f(x)在[-2,4]上的最值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=5x+x-2,g(x)=log5x+x-2的零点分别为x1,x2,则x1+x2的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga(1+x),g(x)=loga(1-x),(a>0,a≠1).
(1)设a=2,函数f(x)的定义域为[3,63],求f(x)的最值;
(2)求使f(x)-g(x)>0的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
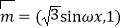 ,
,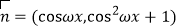 ,设函数
,设函数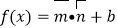 .
.(1)若函数
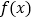 的图象关于直线
的图象关于直线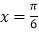 对称,且
对称,且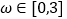 时,求函数
时,求函数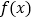 的单调增区间;
的单调增区间;(2)在(1)的条件下,当
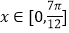 时,函数
时,函数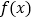 有且只有一个零点,求实数
有且只有一个零点,求实数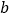 的取值范围.
的取值范围.
相关试题

