【题目】数列{an}满足:a1= ![]() ,前n项和Sn=
,前n项和Sn= ![]() an ,
an ,
(1)写出a2 , a3 , a4;
(2)猜出an的表达式,并用数学归纳法证明.
参考答案:
【答案】
(1)
解:∵ ![]() ,
,
∴令n=2, ![]() ,即a1+a2=3a2.∴
,即a1+a2=3a2.∴ ![]() .
.
令n=3,得 ![]() ,即a1+a2+a3=6a3,∴
,即a1+a2+a3=6a3,∴ ![]() .
.
令n=4,得 ![]() ,a1+a2+a3+a4=10a4,∴
,a1+a2+a3+a4=10a4,∴ ![]()
(2)
解:猜想 ![]() ,下面用数学归纳法给出证明.
,下面用数学归纳法给出证明.
①当n=1时, ![]() 结论成立.
结论成立.
②假设当n=k时,结论成立,即 ![]() ,
,
则当n=k+1时, ![]()
= ![]() ,
,
即 ![]() .
.
∴ ![]()
∴ 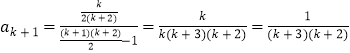 .
.
∴当n=k+1时结论成立.
由①②可知,对一切n∈N+都有 ![]() 成立
成立
【解析】(1)根据 ![]() ,利用递推公式,分别令n=2,3,4.求出a1 , a2 , a3 , a4;(2)根据(1)求出的数列的前四项,从而总结出规律猜出an , 然后利用数学归纳法进行证明即得.
,利用递推公式,分别令n=2,3,4.求出a1 , a2 , a3 , a4;(2)根据(1)求出的数列的前四项,从而总结出规律猜出an , 然后利用数学归纳法进行证明即得.
【考点精析】关于本题考查的数列的通项公式,需要了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为获得较好的收益,每年要投入一定资金用于广告促销,经调查,每年投入广告费
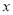 (百万元),可增加销售额约为
(百万元),可增加销售额约为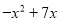 (百万元)(
(百万元)(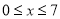 )
)(1)若该公司当年的广告费控制在4百万元之内,则应该设入多少广告费,才能使该公司获得的收益最大?
(2)现该公司准备共投入6百万元,分别用于广告促销售和技术改造,经预测,每设入技术改造费
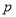 (百万元),可增加销售额约为
(百万元),可增加销售额约为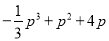 (百万元),请设计一种资金分配方案,使该公司由此获得最大收益.(注:收益
(百万元),请设计一种资金分配方案,使该公司由此获得最大收益.(注:收益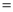 销售额
销售额 成本)
成本) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
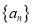 各项均为正数,其前
各项均为正数,其前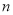 项和为
项和为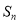 ,且
,且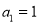 ,
, 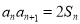 .
.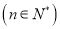
(Ⅰ)求数列
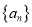 的通项公式;
的通项公式;(Ⅱ)求数列
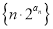 的前
的前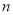 项和
项和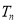 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为60cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax﹣1(a>0,且a≠1),当x∈(0,+∞)时,f(x)>0,且函数g(x)=f(x+1)﹣4的图象不过第二象限,则a的取值范围是( )
A.(1,+∞)
B.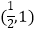
C.(1,3]
D.(1,5] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
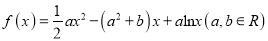
(Ⅰ)当
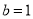 时,求函数
时,求函数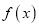 的单调区间;
的单调区间; (Ⅱ)当
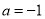 ,
,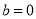 时,证明:
时,证明: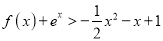 (其中
(其中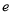 为自然对数的底数).
为自然对数的底数). -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥P﹣ABCD中,底面ABCD是一直角梯形,BA⊥AD,AD∥BC,AB=BC=2,PA=3,AD=6,PA⊥底面ABCD,E是PD上的动点.若CE∥平面PAB,则三棱锥C﹣ABE的体积为( )
A.
B.
C.
D.
相关试题

